Egftnjytyk

Przestrzeń metryczna – zbiór z zadaną na nim metryką, tj. funkcją, która określa odległość między każdą parą elementów tego zbioru.

Przestrzenie metryczne tworzą najogólniejszą klasę zbiorów, w których używa się pojęcia odległości wzorowanej na odległości znanej z przestrzeni euklidesowych (prostej, płaszczyzny czy przestrzeni trójwymiarowej).

Wprowadzone zostały przez Maurice’a Frécheta^[1].

Definicja metryki |

Niech X{displaystyle X} oznacza dowolny niepusty zbiór. Metryką w zbiorze X{displaystyle X} nazywa się funkcję^[2]

d:X×X→[0,+∞),{displaystyle dcolon Xtimes Xto [0,+infty ),}

która dla dowolnych elementów a,b,c{displaystyle a,b,c} tego zbioru spełnia warunki:

1. 
   identyczność nierozróżnialnych
   

   d(a,b)=0⟺a=b,{displaystyle d(a,b)=0iff a=b,}

   
   


2. symetria
   

   d(a,b)=d(b,a),{displaystyle d(a,b)=d(b,a),}

   
   


3. 
   nierówność trójkąta
   

   d(a,b)⩽d(a,c)+d(c,b).{displaystyle d(a,b)leqslant d(a,c)+d(c,b).}

   
   

Gdy d{displaystyle d} jest metryką w zbiorze X,{displaystyle X,} to parę (X,d){displaystyle (X,d)} nazywa się przestrzenią metryczną,

• elementy zbioru X{displaystyle X} nazywa się punktami,
  


• liczbę d(a,b){displaystyle d(a,b)} nazywa się odległością punktu a{displaystyle a} od punktu b.{displaystyle b.}
  

Uwaga 1. |

Niekiedy pomija się warunek nieujemności d(a,b)⩾0{displaystyle d(a,b)geqslant 0} przyjmując d:X×X→R{displaystyle dcolon Xtimes Xto mathbb {R} } zamiast d:X×X→[0,+∞).{displaystyle dcolon Xtimes Xto [0,+infty ).}

Wynika on bowiem z wypisanych wyżej aksjomatów:

0=d(a,a)⩽d(a,b)+d(b,a)=2⋅d(a,b).{displaystyle 0=d(a,a)leqslant d(a,b)+d(b,a)=2cdot d(a,b).}

Uwaga 2. |

Można wyeliminować aksjomat symetrii, gdy zastąpi się warunek trójkąta warunkiem:

d(a,b)⩽d(a,c)+d(b,c).{displaystyle d(a,b)leqslant d(a,c)+d(b,c).}

Dowód:

1) Przyjmując w powyższym warunku c=a{displaystyle c=a} dostaniemy:

d(a,b)⩽d(a,a)+d(b,a)=d(b,a).{displaystyle d(a,b)leqslant d(a,a)+d(b,a)=d(b,a).}

2) Zamieniając w powyższym warunku a{displaystyle a} i b{displaystyle b} oraz przyjmując c=b{displaystyle c=b} dostaniemy:

d(b,a)⩽d(b,b)+d(a,b)=d(a,b).{displaystyle d(b,a)leqslant d(b,b)+d(a,b)=d(a,b).}

3) Z powyższych dwóch nierówności wynika: d(a,b)=d(b,a),{displaystyle d(a,b)=d(b,a),} c.n.d.

Metryki w przestrzeni liniowej |

W przestrzeni liniowej (np. euklidesowej, unormowanej, unitarnej) można wprowadzić różnie zdefiniowane metryki. W wyniku tego przestrzeń nabywa dodatkowej struktury – powstaje przestrzeń metryczna. W poniższych przykładach x=(x1,x2,…,xn){displaystyle mathbf {x} =(x_{1},x_{2},dots ,x_{n})} oraz y=(y1,y2,…,yn){displaystyle mathbf {y} =(y_{1},y_{2},dots ,y_{n})} oznaczają elementy przestrzeni Rn.{displaystyle mathbb {R} ^{n}.}

Metryka euklidesowa |

Metrykę euklidesową w przestrzeni Rn{displaystyle mathbb {R} ^{n}} definiuje się wzorem

de(x,y)=(y1−x1)2+⋯+(yn−xn)2,{displaystyle d_{e}(mathbf {x} ,mathbf {y} )={sqrt {(y_{1}-x_{1})^{2}+dots +(y_{n}-x_{n})^{2}}},}

tzn. jako pierwiastek euklidesowego iloczynu skalarnego różnicy dwóch wektorów przez siebie:

de(x,y)=⟨y−x,y−x⟩.{displaystyle d_{e}(mathbf {x} ,mathbf {y} )={sqrt {langle mathbf {y} -mathbf {x} ,mathbf {y} -mathbf {x} rangle }}.}

W przypadku jednowymiarowym powyższy wzór redukuje się do wartości bezwzględnej różnic współrzędnych punktów x=(x1){displaystyle mathbf {x} =(x_{1})} oraz y=(y1){displaystyle mathbf {y} =(y_{1})}

de(x,y)=|y1−x1|.{displaystyle d_{e}(mathbf {x} ,mathbf {y} )=|y_{1}-x_{1}|.}

Metryka generowana przez normę |

Jeżeli (X,‖⋅‖){displaystyle (X,|cdot |)} jest przestrzenią unormowaną, to jako odległość (metrykę) punktów x,y{displaystyle mathbf {x} ,mathbf {y} } można przyjąć długość (normę) wektora, będącego różnicą wektorów x,y,{displaystyle mathbf {x} ,mathbf {y} ,} tj.

d(x,y)=‖x−y‖{displaystyle d(mathbf {x} ,mathbf {y} )=|mathbf {x} -mathbf {y} |} dla x,y∈X{displaystyle mathbf {x} ,mathbf {y} in X}

Metryka ta jest uogólnieniem metryki euklidesowej. Np. metrykami są funkcje postaci

‖x−y‖p=(|x1−y1|p+|x2−y2|p+…+|xn−yn|p)1/p{displaystyle |mathbf {x} -mathbf {y} |_{p}={big (}|x_{1}-y_{1}|^{p}+|x_{2}-y_{2}|^{p}+ldots +|x_{n}-y_{n}|^{p}{big )}^{1/p}}

gdzie 1⩽p<∞.{displaystyle 1leqslant p<infty .} Metryka ‖⋅‖2{displaystyle |cdot |_{2}} jest metryką euklidesową i oznacza się ją symbolem |⋅|.{displaystyle |cdot |.}

Metrykę, którą definiuje się w oparciu o normę przestrzeni, nazywa się metryką generowaną przez normę.

Metryka maksimum |

	a	b	c	d	e	f	g	h
8									8
7									7
6									6
5									5
4									4
3									3
2									2
1									1
	a	b	c	d	e	f	g	h

 Zobacz też: odległość Czebyszewa.

Metryka maksimum zwana także metryką nieskończoność, maksimum, Czebyszewa, szachową jest określona w przestrzeni Rn{displaystyle mathbb {R} ^{n}} za pomocą wzoru

d∞(x,y)=maxk=1,…,n |xk−yk|{displaystyle d_{infty }(mathbf {x} ,mathbf {y} )=max _{k=1,dots ,n}~|x_{k}-y_{k}|}

– odległość ta jest de facto metryką generowaną przez normę maksimum zadaną wzorem

‖x‖∞=max{|xi|:i=1,…,n}.{displaystyle |mathbf {x} |_{infty }=max {big {}|x_{i}|colon ,i=1,dots ,n{big }}.}

Kula w tej metryce jest kostką n-wymiarową.

Łatwo sprawdzić, że w grze w szachy minimalna liczba ruchów, jakie musi wykonać król, aby przejść z pewnego pola na inne określona jest tą metryką (na rysunku obok pokazano możliwe ruchy króla z danego pola).

Metryka węzła kolejowego |

 Zobacz też: jeż (topologia).

Metryka węzła kolejowego zwana także metryką centrum, kolejową, metra paryskiego może być zdefiniowana na płaszczyźnie.

Niech O{displaystyle O} będzie pewnym ustalonym punktem na płaszczyźnie. Odległość dwóch punktów A,B{displaystyle A,B} w tej metryce wyznacza się następująco:

Jeżeli punkty leżą na prostej przechodzącej przez punkt O,{displaystyle O,} to

dk(A,B)=de(A,B),{displaystyle d_{k}(A,B)=d_{e}(A,B),}

w przeciwnym wypadku

dk(A,B)=de(A,O)+de(O,B).{displaystyle d_{k}(A,B)=d_{e}(A,O)+d_{e}(O,B).}

Metrykę tę można uogólnić na przestrzeń Rn,{displaystyle mathbb {R} ^{n},} w której ustalono pewien jej punkt O.{displaystyle O.}

Metrykę powyższą można też zastosować do labiryntu, w którym wszystkie korytarze są prostymi rozchodzącymi się gwiaździście od jednego punktu O.{displaystyle O.} Przejście z jednego korytarza do drugiego wymaga dotarcia do skrzyżowania (centrum), aby możliwe było skręcenie w docelowy korytarz. Długość pokonanej trasy odpowiada odległości wyliczonej w tej metryce.

Metryka rzeka |

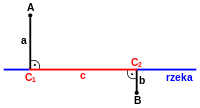
Odległość w metryce rzeka.

Niech r{displaystyle r} będzie ustaloną prostą na płaszczyźnie. Odległość dr(A,B){displaystyle d_{r}(A,B)} punktów A,B{displaystyle A,B} w metryce rzece wyznacza się następująco:

Jeżeli punkty leżą na prostej prostopadłej do prostej r,{displaystyle r,} to

dr(A,B)=de(A,B),{displaystyle d_{r}(A,B)=d_{e}(A,B),}

w przeciwnym wypadku

dr(A,B)=de(A,C1)+de(C1,C2)+de(C2,B).{displaystyle d_{r}(A,B)=d_{e}(A,C_{1})+d_{e}(C_{1},C_{2})+d_{e}(C_{2},B).}

gdzie C1,C2{displaystyle C_{1},C_{2}} są rzutami prostopadłymi punktów odpowiednio A,B{displaystyle A,B} na prostą r.{displaystyle r.}

Metrykę tę można uogólnić na przestrzeń Rn,{displaystyle mathbb {R} ^{n},} w której ustalono pewną jej prostą r.{displaystyle r.}

Metrykę tą można zastosować np. do mierzenia trasy pokonanej drogą wodną w sieci złożonej z rzeki i licznych, prostopadłych jej dopływów (por. rysunek).

Uogólniona metryka rzeka |

Dalsze uogólnienie tej i poprzedniej metryki w Rn{displaystyle mathbb {R} ^{n}} można uzyskać przyjmując zamiast punktu i prostej rozmaitość liniową r{displaystyle mathbb {r} } wymiaru a spełniającego 0≤a<n.{displaystyle 0leq a<n.} Niech ponadto 0<b<n,{displaystyle 0<b<n,} przy czym a+b≤n.{displaystyle a+bleq n.}

Jeżeli punkty A,B{displaystyle A,B} leżą na pewnej rozmaitości wymiaru b{displaystyle b} prostopadłej do rozmaitości r,{displaystyle r,} to

dr(A,B)=de(A,B),{displaystyle d_{r}(A,B)=d_{e}(A,B),}

w przeciwnym wypadku

dr(A,B)=de(A,C1)+de(C1,C2)+de(C2,B).{displaystyle d_{r}(A,B)=d_{e}(A,C_{1})+d_{e}(C_{1},C_{2})+d_{e}(C_{2},B).}

gdzie C1,C2{displaystyle C_{1},C_{2}} są rzutami prostopadłymi punktów odpowiednio A,B{displaystyle A,B} na prostą r.{displaystyle r.}

Dla a=1, b=1 jest to metryka rzeka, dla a=0, b=1 jest to metryka węzła kolejowego

Metryka dyskretna |

Metrykę dyskretną zwaną także metryką zero-jedynkową wprowadzić można w dowolnym niepustym zbiorze. Odległość dd(x,y){displaystyle d_{d}(x,y)} punktów x{displaystyle x} oraz y{displaystyle y} zbioru X{displaystyle X} określa wzór^[3]

dd(x,y)={0,gdy x=y,1,gdy x≠y.{displaystyle d_{d}(x,y)={begin{cases}0,&{text{gdy }}x=y,\1,&{text{gdy }}xneq y.end{cases}}}

Parę X{displaystyle X} z metryką dd{displaystyle d_{d}} nazywa się przestrzenią metryczną dyskretną.

Porównanie metryk przytoczonych w przykładach |

Dla n=1{displaystyle n=1} metryki euklidesowa, Manhattan, szachowa pokrywają się. Jeżeli n=2,{displaystyle n=2,} to metryki szachowa i Manhattan nie pokrywają się, ale czynią z płaszczyzny przestrzenie izometryczne (tzn. izomorficzne metrycznie, czyli nierozróżnialne metrycznie), gdyż w obu przypadkach kulami są kwadraty z przestrzeni euklidesowej, ale o różnym położeniu (odpowiednio o bokach równoległych do osi oraz obróconych względem osi o 45°).

Metryka w przestrzeniach pseudoriemannowskich |

Powierzchnia sfery, elipsoidy obrotowej, hiperboloidy obrotowej, czy też 4-wymiarowa czasoprzestrzeń opisywana w ogólnej teorii względności są przykładami przestrzeni nieeuklidesowych, które określa się jako rozmaitości riemannowskie i najogólniejsze – rozmaitości pseudoriemannowskie.

Nie da się w ogólnym przypadku wprowadzić tu metryki opisanej prostym wzorem, tak jak w przestrzeniach liniowych, np. w przestrzeni euklidesowej. Podstawową rolę gra tu tensor metryczny.

Niech M{displaystyle M} będzie rozmaitością wymiaru n{displaystyle n} i niech dany będzie układ współrzędnych krzywoliniowych, tak że każdy punkt rozmaitości ma określone współrzędne krzywoliniowe x=(x1,…,xn).{displaystyle mathbf {x} =(x^{1},dots ,x^{n}).}

Odległość infinitezymalna |

Tensor metryczny definiuje infinitezymalne odległości między punktami: długość wektora dx=(dx1,…,dxn){displaystyle dmathbf {x} =(dx^{1},dots ,dx^{n})} łączącego punkt x{displaystyle mathbf {x} } z infinitezymalnie odległym punktem y=x+dx{displaystyle mathbf {y} =mathbf {x} +dmathbf {x} } zadana jest wzorem

|dx|=|∑i,j=1ngij(x)dxidxj|{displaystyle |dmathbf {x} |={sqrt {{Bigg |}sum _{i,j=1}^{n}g_{ij}(mathbf {x} )dx^{i}dx^{j}{Bigg |}}}}

gdzie:

gij(x),i,j=1,…,n{displaystyle g_{ij}(mathbf {x} ),i,j=1,dots ,n}

– współrzędne tensora metrycznego (będące funkcjami położenia x{displaystyle mathbf {x} })

Odległość dowolnych punktów |

Dla punktów x,y{displaystyle mathbf {x,y} } rozmaitości M{displaystyle M} dowolnie odległych metrykę definiuje się jako kres dolny zbioru, zawierającego długości krzywych γ{displaystyle gamma } ciągłych i różniczkowalnych, łączących punkty x,y,{displaystyle mathbf {x,y} ,} czyli

d(x,y)=inf{L(γ),γ∈M,γ(a)=x,γ(b)=y}{displaystyle d(mathbf {x,y} )=inf ,{,L(gamma ),{gamma }in M,,gamma (a)=mathbf {x} ,gamma (b)=mathbf {y} }}

gdzie:

• 
  inf{...}{displaystyle inf ,{...}} = infimum = kres dolny zbioru


• 
  L(γ)=∫ab|∑i,j=1ngij(γ(t))dγi(t)dtdγj(t)dt|dt{displaystyle L(gamma )=int limits _{a}^{b}{sqrt {{Bigg |}sum _{i,j=1}^{n}g_{ij}(gamma (t)){frac {dgamma ^{i}(t)}{dt}}{frac {dgamma ^{j}(t)}{dt}}{Bigg |}}},dt} – długość krzywej γ{displaystyle gamma }
  

przy czym krzywa γ{displaystyle gamma } dana jest przez n{displaystyle n} równań parametrycznych

γ(t)=[γ1(t),…,γn(t)],{displaystyle gamma (t)=[gamma ^{1}(t),dots ,gamma ^{n}(t)],} t∈⟨a,b⟩{displaystyle tin langle a,brangle }

oraz

γ(a)=x,γ(b)=y{displaystyle gamma (a)=mathbf {x} ,,,gamma (b)=mathbf {y} }

Dla przestrzeni riemannowskich odległość punktów jest wyznaczona przez łuk krzywej geodezyjnej. Dla sfery będzie to łuk koła wielkiego, na którym leżą dwa punkty. A np. dla czasoprzestrzeni, która jest 4-wymiarową przestrzenią pseudoriemannowską, odległość może być zerowa, jeśli łączy dwa punkty – tzw. zdarzenia czasoprzestrzenne – które są związane z rozchodzeniem się sygnału świetlnego.

Topologia przestrzeni metrycznej |

Przestrzeń metryczną X{displaystyle X} łatwo jest przekształcić w przestrzeń topologiczną, definiując następująco topologię:

a) bazę topologii stanowi rodzina wszystkich kul otwartych, tj. zbiorów postaci

B(x,r)={y∈X:d(x,y)<r},{displaystyle B(x,r)={yin Xcolon ,d,(x,y)<r},}

gdzie x{displaystyle x} – dowolny elementem przestrzeni X,{displaystyle X,} r{displaystyle r} – promień kuli (r>0),{displaystyle (r>0),}

b) podzbiór U{displaystyle U} przestrzeni X{displaystyle X} należy do topologii (czyli jest zbiorem otwartym), jeżeli jest sumą kul otwartych.

Taką topologię nazywa się topologią generowaną na zbiorze X{displaystyle X} przez metrykę d.{displaystyle d.}

Metryzowalna przestrzeń topologiczna |

 Osobny artykuł: Twierdzenia o metryzacji.

Przestrzeń topologiczną (X,τ){displaystyle (X,tau )} nazywamy przestrzenią metryzowalną, jeśli da się w niej wprowadzić topologię generowaną przez jakąś metrykę. Przykładami twierdzeń dotyczących metryzacji przestrzeni topologicznych są:

• 
  twierdzenie Nagaty-Smirnowa,


• 
  twierdzenie Binga.

Z punktu widzenia topologii metryki służą badaniu przestrzeni metryzowalnych (analogicznie jak układy współrzędnych służą badaniu przestrzeni euklidesowych).

Własności przestrzeni metrycznych |

Tw. 1 Każda przestrzeń metryczna jest

• 
  parazwarta,


• 
  doskonale normalna,


• 
  Hausdorffa,


• spełnia pierwszy aksjomat przeliczalności.

Tw. 2 Poniższe niezmienniki topologiczne są równoważne w przestrzeniach metrycznych:

• 
  drugi aksjomat przeliczalności, ośrodkowość, własność Lindelöfa,


• 
  zwartość, ciągowa zwartość, przeliczalna zwartość.

Definicja odległości punktu od zbioru |

 Osobny artykuł: metryka Hausdorffa.

Odległością (odstępem) punktu x{displaystyle x} od zbioru A{displaystyle A} nazywa się funkcję

δA(x)=inf{d(x,a):a∈A}.{displaystyle delta _{A}(x)=inf {big {}d(x,a)colon ain A{big }}.}

Równoważność metryk |

Definicja |

Niech (X,d1),(X,d2){displaystyle (X,d_{1}),(X,d_{2})} będą przestrzeniami metrycznymi.

Df. 1 Metryki d1,d2{displaystyle d_{1},d_{2}} nazywa się równoważnymi topologicznie, jeżeli granice dowolnych ciągów obliczone z użyciem tych metryk są identyczne^[4].

Df. 2 Metryki d1,d2{displaystyle d_{1},d_{2}} nazywa się równoważnymi lipschitzowsko, jeżeli istnieją stałe c,C>0,{displaystyle c,,C,>0,} takie że dla każdego x,y∈X{displaystyle x,yin X} spełniony jest warunek

c⋅d1(x,y)⩽d2(x,y)⩽C⋅d1(x,y).{displaystyle ccdot d_{1}(x,y)leqslant d_{2}(x,y)leqslant Ccdot d_{1}(x,y).}

Twierdzenia o metrykach równoważnych |

Tw. 1 Metryki równoważne lipschitzowsko są równoważne topologicznie: jeśli pewien ciąg elementów zbioru X{displaystyle X} jest zbieżny w sensie metryki d1,{displaystyle d_{1},} to jest także zbieżny w sensie metryki d2.{displaystyle d_{2}.}

Tw. 2 W rzeczywistej przestrzeni liniowej skończonego wymiaru wszystkie metryki indukowane przez normy Banacha są równoważne lipschitzowsko, a więc i topologicznie.

Tw. 3 Gdy dwie normy Banacha zdefiniowane na tej samej przestrzeni liniowej są topologicznie równoważne, to są one także równoważne lipschitzowsko.

Metryka niezmiennicza na przesunięcia |

Metrykę d{displaystyle d} nazywa się niezmienniczą ze względu na przesunięcia, jeśli na przestrzeni metrycznej X{displaystyle X} określone jest działanie dodawania +:X×X→X{displaystyle +colon Xtimes Xto X} i dla dowolnych punktów a,x,y∈X{displaystyle a,x,yin X} zachodzi warunek

d(x,y)=d(x+a,y+a).{displaystyle d(x,y)=d(x+a,y+a).}

Uogólnienia |

Rozpatruje się wiele funkcji spełniających podobne układy aksjomatów:

• zastępując aksjomat identyczności nierozróżnialnych następującym

d(a,a)=0{displaystyle d(a,a)=0}

uzyskuje się tzw. pseudometrykę.

• rezygnując z aksjomatu symetrii uzyskuje się quasi-metryką
  


• zastępując warunek trójkąta aksjomatem

d(a,b)⩽max{d(a,c),d(c,b)}{displaystyle d(a,b)leqslant max {big {}d(a,c),d(c,b){big }}} uzyskuje się funkcję nazywaną ultrametryką.

Zobacz też |

Inne typy metryk:

• metryka euklidesowa


• metryka pomiarowa


• metryka probabilistyczna


• metryka riemannowska


• metryka Czebyszewa


• metryka Friedmana-Lemaître’a-Robertsona-Walkera


• metryka Hausdorffa


• metryka Mahalanobisa


• metryka Minkowskiego


• metryka Schwarzschilda

Pseudometryki:

• pseudometryka pseudoriemannowska

Przestrzenie metryzowalne:

• przestrzeń topologiczna


• przestrzeń unormowana


• przestrzeń pseudometryczna

Przypisy |

Bibliografia |

• Wacław Sierpiński: Wstęp do teorii mnogości i topologii. Warszawa: Państwowe Zakłady Wydawnictw Szkolnych, 1965, s. 131.


• Ryszard Engelking: Topologia ogólna. Warszawa: PWN, 1975.


• Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. drugie, zmienione. Warszawa: PWN, 1962.


• Kołodziej Witold: Analiza matematyczna. PWN, Warszawa 2009.


• Athanase Papadopoulos, Metric Spaces, Convexity and Nonpositive Curvature, European Mathematical Society, 2004, ​ISBN 978-3-03719-010-4​.