Fatigue (material)
In materials science, fatigue is the weakening of a material caused by repeatedly applied loads. It is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. The nominal maximum stress values that cause such damage may be much less than the strength of the material typically quoted as the ultimate tensile stress limit, or the yield stress limit.
Fatigue occurs when a material is subjected to repeated loading and unloading. If the loads are above a certain threshold, microscopic cracks will begin to form at the stress concentrators such as the surface, persistent slip bands (PSBs), interfaces of constituents in the case of composites, and grain interfaces in the case of metals.[1] Eventually a crack will reach a critical size, the crack will propagate suddenly, and the structure will fracture. The shape of the structure will significantly affect the fatigue life; square holes or sharp corners will lead to elevated local stresses where fatigue cracks can initiate. Round holes and smooth transitions or fillets will increase the fatigue strength of the structure.
Contents
1 Fatigue life
2 Characteristics of fatigue
3 Timeline of fatigue research history
4 High-cycle fatigue
4.1 Stress-cycle (S-N) curve
4.2 Probabilistic nature of fatigue
4.3 Complex loadings
4.3.1 For multiaxial loading
4.4 Miner's Rule
4.5 Constant Fatigue Life (CFL) diagram and Goodman relation
4.6 Paris' Law
4.7 Strain-cycle (ε-N) curve
5 Low-cycle fatigue
6 Fatigue and fracture mechanics
6.1 Crack initiation
7 Design against fatigue
7.1 Stopping fatigue
7.2 Material change
7.3 Peening treatment of welds and metal components
7.3.1 Deep Cryogenic treatment
8 Notable fatigue failures
8.1 Versailles train crash
8.2 de Havilland Comet
8.3 Alexander L. Kielland oil platform capsizing
8.4 Others
9 See also
10 References
11 Further reading
12 External links
Fatigue life
The American Society for Testing and Materials defines fatigue life, Nf, as the number of stress cycles of a specified character that a specimen sustains before failure of a specified nature occurs.[2] For some materials, notably steel and titanium, there is a theoretical value for stress amplitude below which the material will not fail for any number of cycles, called a fatigue limit, endurance limit, or fatigue strength.[3]
Engineers have used any of three methods to determine the fatigue life of a material: the stress-life method, the strain-life method, and the linear-elastic fracture mechanics method.[4] One method to predict fatigue life of materials is the Uniform Material Law (UML).[5] UML was developed for fatigue life prediction of aluminium and titanium alloys by the end of 20th century and extended to high-strength steels,[6] and cast iron.[7]
Characteristics of fatigue

Fracture of an aluminium crank arm. Dark area of striations: slow crack growth. Bright granular area: sudden fracture.
- In metal alloys, and for the simplifying case when there are no macroscopic or microscopic discontinuities, the process starts with dislocation movements at the microscopic level, which eventually form persistent slip bands that become the nucleus of short cracks.
- Macroscopic and microscopic discontinuities (at the crystalline grain scale) as well as component design features which cause stress concentrations (holes, keyways, sharp changes of load direction etc.) are common locations at which the fatigue process begins.
- Fatigue is a process that has a degree of randomness (stochastic), often showing considerable scatter even in seemingly identical samples in well controlled environments.
- Fatigue is usually associated with tensile stresses but fatigue cracks have been reported due to compressive loads.[8]
- The greater the applied stress range, the shorter the life.
- Fatigue life scatter tends to increase for longer fatigue lives.
- Damage is cumulative. Materials do not recover when rested.
- Fatigue life is influenced by a variety of factors, such as temperature, surface finish, metallurgical microstructure, presence of oxidizing or inert chemicals, residual stresses, scuffing contact (fretting), etc.
- Some materials (e.g., some steel and titanium alloys) exhibit a theoretical fatigue limit below which continued loading does not lead to fatigue failure.
- High cycle fatigue strength (about 104 to 108 cycles) can be described by stress-based parameters. A load-controlled servo-hydraulic test rig is commonly used in these tests, with frequencies of around 20–50 Hz. Other sorts of machines—like resonant magnetic machines—can also be used, to achieve frequencies up to 250 Hz.
Low cycle fatigue (loading that typically causes failure in less than 104 cycles) is associated with localized plastic behavior in metals; thus, a strain-based parameter should be used for fatigue life prediction in metals. Testing is conducted with constant strain amplitudes typically at 0.01–5 Hz.
Timeline of fatigue research history
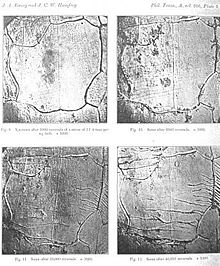
Micrographs showing how surface fatigue cracks grow as material is further cycled. From Ewing & Humfrey, 1903
- 1837: Wilhelm Albert publishes the first article on fatigue. He devised a test machine for conveyor chains used in the Clausthal mines.[9]
- 1839: Jean-Victor Poncelet describes metals as being 'tired' in his lectures at the military school at Metz.
- 1842: William John Macquorn Rankine recognises the importance of stress concentrations in his investigation of railroad axle failures. The Versailles train wreck was caused by fatigue failure of a locomotive axle.[10]
- 1843: Joseph Glynn reports on the fatigue of an axle on a locomotive tender. He identifies the keyway as the crack origin.
- 1848: The Railway Inspectorate reports one of the first tyre failures, probably from a rivet hole in tread of railway carriage wheel. It was likely a fatigue failure.
- 1849: Eaton Hodgkinson is granted a "small sum of money" to report to the UK Parliament on his work in "ascertaining by direct experiment, the effects of continued changes of load upon iron structures and to what extent they could be loaded without danger to their ultimate security".
- 1854: Braithwaite reports on common service fatigue failures and coins the term fatigue.[11]
- 1860: Systematic fatigue testing undertaken by Sir William Fairbairn and August Wöhler.
- 1870: Wöhler summarises his work on railroad axles. He concludes that cyclic stress range is more important than peak stress and introduces the concept of endurance limit.[9]
- 1903: Sir James Alfred Ewing demonstrates the origin of fatigue failure in microscopic cracks.
- 1910: O. H. Basquin proposes a log-log relationship for S-N curves, using Wöhler's test data.[12]
- 1940: Sidney M. Cadwell publishes first rigorous study of fatigue in rubber.[13]
- 1945: A. M. Miner popularises Palmgren's (1924) linear damage hypothesis as a practical design tool.
- 1952: W. Weibull An S-N curve model.[14]
- 1954: The world's first commercial jetliner, the de Havilland Comet, suffers disaster as three planes break up in mid-air, causing de Havilland and all other manufacturers to redesign high altitude aircraft and in particular replace square apertures like windows with oval ones.
- 1954: L. F. Coffin and S. S. Manson explain fatigue crack-growth in terms of plastic strain in the tip of cracks.
- 1961: P. C. Paris proposes methods for predicting the rate of growth of individual fatigue cracks in the face of initial scepticism and popular defence of Miner's phenomenological approach.
- 1968: Tatsuo Endo and M. Matsuishi devise the rainflow-counting algorithm and enable the reliable application of Miner's rule to random loadings.[15]
- 1970: W. Elber elucidates the mechanisms and importance of crack closure in slowing the growth of a fatigue crack due to the wedging effect of plastic deformation left behind the tip of the crack.
- 1973: M. W. Brown and K. J. Miller observe that fatigue life under multiaxial conditions is governed by the experience of the plane receiving the most damage, and that both tension and shear loads on the critical plane must be considered.[16]
High-cycle fatigue
Historically, most attention has focused on situations that require more than 104 cycles to failure where stress is low and primarily elastic.
Stress-cycle (S-N) curve
In high-cycle fatigue situations, materials performance is commonly characterized by an S-N curve, also known as a Wöhler curve . This is a graph of the magnitude of a cyclic stress (S) against the logarithmic scale of cycles to failure (N).[17]

S-N curve for a brittle aluminium with an ultimate tensile strength of 320 MPa
S-N curves are derived from tests on samples of the material to be characterized (often called coupons) where a regular sinusoidal stress is applied by a testing machine which also counts the number of cycles to failure. This process is sometimes known as coupon testing. For greater accuracy but lower generality component testing is used.[18] Each coupon or component test generates a point on the plot though in some cases there is a runout where the time to failure exceeds that available for the test (see censoring). Analysis of fatigue data requires techniques from statistics, especially survival analysis and linear regression.
The progression of the S-N curve can be influenced by many factors such as stress ratio (mean stress), loading frequency, temperature, corrosion, residual stresses, and the presence of notches. A constant fatigue life (CFL) diagram[19] is useful for the study of stress ratio effect. The Goodman-Line is a method used to estimate the influence of the mean stress on the fatigue strength.
Probabilistic nature of fatigue
As coupons sampled from a homogeneous frame will display a variation in their number of cycles to failure, the S-N curve should more properly be a Stress-Cycle-Probability (S-N-P) curve to capture the probability of failure after a given number of cycles of a certain stress. Probability distributions that are common in data analysis and in design against fatigue include the log-normal distribution, extreme value distribution, Birnbaum–Saunders distribution, and Weibull distribution.
Complex loadings

Spectrum loading
In practice, a mechanical part is exposed to a complex, often random, sequence of loads, large and small. In order to assess the safe life of such a part:
- Complex loading is reduced to a series of simple cyclic loadings using a technique such as rainflow analysis;
- A histogram of cyclic stress is created from the rainflow analysis to form a fatigue damage spectrum;
- For each stress level, the degree of cumulative damage is calculated from the S-N curve; and
- The effect of the individual contributions are combined using an algorithm such as Miner's rule.
For multiaxial loading
Since S-N curves are typically generated for uniaxial loading, some equivalence rule is needed whenever the loading is multiaxial. For simple, proportional loading histories (lateral load in a constant ratio with the axial), Sines rule may be applied. For more complex situations, such as nonproportional loading, critical plane analysis must be applied.
Miner's Rule
In 1945, M. A. Miner[20] popularised a rule that had first been proposed by A. Palmgren in 1924. The rule, variously called Miner's rule or the Palmgren-Miner linear damage hypothesis, states that where there are k different stress magnitudes in a spectrum, Si (1 ≤ i ≤ k), each contributing ni(Si) cycles, then if Ni(Si) is the number of cycles to failure of a constant stress reversal Si (determined by uni-axial fatigue tests), failure occurs when:
- ∑i=1kniNi=C{displaystyle sum _{i=1}^{k}{frac {n_{i}}{N_{i}}}=C}
Usually, for design purposes, C is assumed to be 1. This can be thought of as assessing what proportion of life is consumed by a linear combination of stress reversals at varying magnitudes.
Although Miner's rule may be a useful approximation in many circumstances, it has several major limitations:
- It fails to recognize the probabilistic nature of fatigue and there is no simple way to relate life predicted by the rule with the characteristics of a probability distribution. Industry analysts often use design curves, adjusted to account for scatter, to calculate Ni(Si).
- The sequence in which high vs. low stress cycles are applied to a sample in fact affect the fatigue life, for which Miner's Rule does not account. In some circumstances, cycles of low stress followed by high stress cause more damage than would be predicted by the rule.[21] It does not consider the effect of an overload or high stress which may result in a compressive residual stress that may retard crack growth. High stress followed by low stress may have less damage due to the presence of compressive residual stress.
Constant Fatigue Life (CFL) diagram and Goodman relation
A CFL diagram is useful for stress ratio effect on S-N curve.[22] Also, in the presence of a steady stress superimposed on the cyclic loading, the Goodman relation can be used to estimate a failure condition. It plots stress amplitude against mean stress with the fatigue limit and the ultimate tensile strength of the material as the two extremes. Alternative failure criteria include Soderberg and Gerber.[23]
Paris' Law

Typical fatigue crack growth rate graph
In Fracture mechanics, Anderson, Gomez, and Paris derived relationships for the stage II crack growth with cycles N, in terms of the cyclical component ΔK of the Stress Intensity Factor K[24]
- dadN=C(ΔK)m{displaystyle {frac {mathrm {d} a}{mathrm {d} N}}=C(Delta K)^{m}}
where a is the crack length and m is typically in the range 3 to 5 (for metals), which states that the rate of crack growth with respect to the cycles of load applied is a function of the stress intensity factor; this is named Paris' law.
This relationship was later modified by Forman in 1967[25] to make better allowance for the mean stress, by introducing a factor depending on (1 − R) where R = min stress/max stress, in the denominator.
Strain-cycle (ε-N) curve
Due to the proportionality between stress and strain, high cycle fatigue can also be expressed as strain amplitude vs. number of cycles. High cycle fatigue can be approximated by equating the total strain to just the elastic strain. Using this approximation,
- 1⁄2Δεelastic ≡ σf'⁄E(2Nf)−b
where
- Δεelastic is the change in elastic strain per cycle
- σf' is a parameter that scales with tensile strength obtained by fitting experimental data
E is the Young's modulus
Nf is the number of cycles to failure
b is the slope of the log-log curve again determined by fitting
The figure below shows high cycle fatigue as the right-most linear portion. Any test performed in the bottom left region (i.e. with a low enough strain amplitude and number of cycles) below the dark line has a high probability to avoid failure.

Graph showing fatigue failure as a function of strain amplitude.
As shown in the figure above (the left-most linear section) and as described in the next section, the total strain is approximated to be equal to just the plastic strain. For regions between high and low cycle fatigue, an unweighted sum of the high cycle and low cycle expressions gives a reasonable approximation with a built-in safety factor.[26]
Low-cycle fatigue
Where the stress is high enough for plastic deformation to occur, the accounting of the loading in terms of stress is less useful and the strain in the material offers a simpler and more accurate description. This type of fatigue is normally experienced by components which undergo a relatively small number of straining cycles. Low-cycle fatigue is usually characterised by the Coffin-Manson relation (published independently by L. F. Coffin in 1954[27] and S. S. Manson in 1953):[28]
- Δεp2=εf′(2N)c{displaystyle {frac {Delta varepsilon _{p}}{2}}=varepsilon _{f}'(2N)^{c}}
where,
- Δεp /2 is the plastic strain amplitude;
- εf' is an empirical constant known as the fatigue ductility coefficient, the failure strain for a single reversal;
- 2N is the number of reversals to failure (N cycles);
c is an empirical constant known as the fatigue ductility exponent, commonly ranging from −0.5 to −0.7 for metals in time independent fatigue. Slopes can be considerably steeper in the presence of creep or environmental interactions.
A similar relationship for materials such as Zirconium is used in the nuclear industry.[29]
Fatigue and fracture mechanics
Fatigue failures, both for high and low cycle, all follow the same basic steps process of crack initiation, stage I crack growth, stage II crack growth, and finally ultimate failure. To begin the process cracks must nucleate within a material. This process can occur either at stress risers in metallic samples or at areas with a high void density in polymer samples. These cracks propagate slowly at first during stage I crack growth along crystallographic planes, where shear stresses are highest. Once the cracks reach a critical size they propagate quickly during stage II crack growth in a direction perpendicular to the applied force. These cracks can eventually lead to the ultimate failure of the material, often in a brittle catastrophic fashion.
Crack initiation
The formation of initial cracks preceding fatigue failure is a separate process consisting of four discrete steps in metallic samples. The material will develop cell structures and harden in response to the applied load. This causes the amplitude of the applied stress to increase given the new restraints on strain. These newly formed cell structures will eventually break down with the formation of persistent slip bands (PSBs). Slip in the material is localized at these PSBs, and the exaggerated slip can now serve as a stress concentrator for a crack to form. Nucleation of a crack to a detectable size accounts for most of the cracking process. It is for this reason that cyclic fatigue failures seem to occur so suddenly- the bulk of the changes in the material are not visible without destructive testing. Even in normally ductile materials, fatigue failures will resemble sudden brittle failures.
PSB-induced slip planes result in intrusions and extrusions along the surface of a material, often occurring in pairs. This slip is not a microstructural change within the material, but rather a propagation of dislocations within the material. Instead of a smooth interface, the intrusions and extrusions will cause the surface of the material to resemble the edge of a deck of cards, where not all cards are perfectly aligned. Slip-induced intrusions and extrusions create extremely fine surface structures on the material. With surface structure size inversely related to stress concentration factors, PSB-induced surface slip quickly becomes a perfect place for fractures to initiate.
It should be noted that these steps can be bypassed entirely if the cracks form at a preexisting stress concentrator either from an inclusion in the material or from a geometric stress concentrator such as a sharp corner or small radius. Forming a PSB before failure requires more energy than crack initiation at a preexisting stress concentrator. It is for that reason that part design and material quality must be scrutinized when producing parts that will be subjected to high cycle loading.

Fracture surface in a glass rod showing beach marks surrounding the initiation site.
Sources:[30][31]
Design against fatigue
Dependable design against fatigue-failure requires thorough education and supervised experience in structural engineering, mechanical engineering, or materials science. There are four principal approaches to life assurance for mechanical parts that display increasing degrees of sophistication:[32]
- Design to keep stress below threshold of fatigue limit (infinite lifetime concept);
Fail-safe, graceful degradation, and fault-tolerant design: Instruct the user to replace parts when they fail. Design in such a way that there is no single point of failure, and so that when any one part completely fails, it does not lead to catastrophic failure of the entire system.
Safe-life design: Design (conservatively) for a fixed life after which the user is instructed to replace the part with a new one (a so-called lifed part, finite lifetime concept, or "safe-life" design practice); planned obsolescence and disposable product are variants that design for a fixed life after which the user is instructed to replace the entire device;
Damage tolerant design: Instruct the user to inspect the part periodically for cracks and to replace the part once a crack exceeds a critical length. This approach usually uses the technologies of nondestructive testing and requires an accurate prediction of the rate of crack-growth between inspections. The designer sets some aircraft maintenance checks schedule frequent enough that parts are replaced while the crack is still in the "slow growth" phase. This is often referred to as damage tolerant design or "retirement-for-cause".
Stopping fatigue
Fatigue cracks that have begun to propagate can sometimes be stopped by drilling holes, called drill stops, in the path of the fatigue crack.[33] This is not recommended as a general practice because the hole represents a stress concentration factor which depends on the size of the hole and geometry, though the hole is typically less of a stress concentration than the removed tip of the crack. The possibility remains of a new crack starting in the side of the hole. It is always far better to replace the cracked part entirely.
Material change
Changes in the materials used in parts can also improve fatigue life. For example, parts can be made from better fatigue rated metals. Complete replacement and redesign of parts can also reduce if not eliminate fatigue problems. Thus helicopter rotor blades and propellers in metal are being replaced by composite equivalents. They are not only lighter, but also much more resistant to fatigue. They are more expensive, but the extra cost is amply repaid by their greater integrity, since loss of a rotor blade usually leads to total loss of the aircraft. A similar argument has been made for replacement of metal fuselages, wings and tails of aircraft.[34]
Peening treatment of welds and metal components

Example of a HFMI treated steel highway bridge to avoid fatigue along the weld transition.
When a liquid freezes, the last part to freeze develops tensile residual stress as it tries to shrink thermally while remaining rigidly attached to its already-solid surroundings. Welds, which melt a very small portion of a large structure, are particularly prone to this, and are often the starting point of cracks.
Peening a surface can reduce such tensile stresses and create compressive residual stress, which prevents crack initiation. Forms of peening include:
shot peening, using high-speed projectiles
high-frequency impact treatment (also called high-frequency mechanical impact) using a mechanical hammer,[35][36]
laser peening which uses high-energy laser pulses to generate the "hammer blows".
Increases in fatigue life and strength are proportionally related to the depth of the compressive residual stresses imparted. Shot peening imparts compressive residual stresses approximately 0.005 inches (0.1 mm) deep, while laser peening can go 0.040 to 0.100 inches (1 to 2.5 mm) deep, or deeper.[37][not in citation given]
Deep Cryogenic treatment
The use of Deep Cryogenic treatment has been shown to increase resistance to fatigue failure. Springs used in industry, auto racing and firearms have been shown to last up to six times longer when treated. Heat checking, which is a form of thermal cyclic fatigue has been greatly delayed.[38]
Notable fatigue failures
Versailles train crash

left Versailles train disaster

right Drawing of a fatigue failure in an axle by Joseph Glynn, 1843
Following the King Louis-Philippe I's celebrations at the Palace of Versailles, a train returning to Paris crashed in May 1842 at Meudon after the leading locomotive broke an axle. The carriages behind piled into the wrecked engines and caught fire. At least 55 passengers were killed trapped in the carriages, including the explorer Jules Dumont d'Urville. This accident is known in France as the "Catastrophe ferroviaire de Meudon". The accident was witnessed by the British locomotive engineer Joseph Locke and widely reported in Britain. It was discussed extensively by engineers, who sought an explanation.
The derailment had been the result of a broken locomotive axle. Rankine's investigation of broken axles in Britain highlighted the importance of stress concentration, and the mechanism of crack growth with repeated loading. His and other papers suggesting a crack growth mechanism through repeated stressing, however, were ignored, and fatigue failures occurred at an ever-increasing rate on the expanding railway system. Other spurious theories seemed to be more acceptable, such as the idea that the metal had somehow "crystallized". The notion was based on the crystalline appearance of the fast fracture region of the crack surface, but ignored the fact that the metal was already highly crystalline.
de Havilland Comet

The recovered (shaded) parts of the wreckage of G-ALYP and the site (arrowed) of the failure
Two de Havilland Comet passenger jets broke up in mid-air and crashed within a few months of each other in 1954. As a result, systematic tests were conducted on a fuselage immersed and pressurised in a water tank. After the equivalent of 3,000 flights, investigators at the Royal Aircraft Establishment (RAE) were able to conclude that the crash had been due to failure of the pressure cabin at the forward Automatic Direction Finder window in the roof. This 'window' was in fact one of two apertures for the aerials of an electronic navigation system in which opaque fibreglass panels took the place of the window 'glass'. The failure was a result of metal fatigue caused by the repeated pressurisation and de-pressurisation of the aircraft cabin. Also, the supports around the windows were riveted, not bonded, as the original specifications for the aircraft had called for. The problem was exacerbated by the punch rivet construction technique employed. Unlike drill riveting, the imperfect nature of the hole created by punch riveting caused manufacturing defect cracks which may have caused the start of fatigue cracks around the rivet.

The fuselage roof fragment of G-ALYP on display in the Science Museum in London, showing the two ADF windows at-which the initial failure occurred.[39]
The Comet's pressure cabin had been designed to a safety factor comfortably in excess of that required by British Civil Airworthiness Requirements (2.5 times the cabin proof test pressure as opposed to the requirement of 1.33 times and an ultimate load of 2.0 times the cabin pressure) and the accident caused a revision in the estimates of the safe loading strength requirements of airliner pressure cabins.
In addition, it was discovered that the stresses around pressure cabin apertures were considerably higher than had been anticipated, especially around sharp-cornered cut-outs, such as windows. As a result, all future jet airliners would feature windows with rounded corners, greatly reducing the stress concentration. This was a noticeable distinguishing feature of all later models of the Comet. Investigators from the RAE told a public inquiry that the sharp corners near the Comets' window openings acted as initiation sites for cracks. The skin of the aircraft was also too thin, and cracks from manufacturing stresses were present at the corners.
Alexander L. Kielland oil platform capsizing

Fractures on the right side of the Alexander L. Kielland rig
The Alexander L. Kielland was a Norwegian semi-submersible drilling rig that capsized whilst working in the Ekofisk oil field in March 1980, killing 123 people. The capsizing was the worst disaster in Norwegian waters since World War II. The rig, located approximately 320 km east of Dundee, Scotland, was owned by the Stavanger Drilling Company of Norway and was on hire to the United States company Phillips Petroleum at the time of the disaster. In driving rain and mist, early in the evening of 27 March 1980 more than 200 men were off duty in the accommodation on the Alexander L. Kielland. The wind was gusting to 40 knots with waves up to 12 m high. The rig had just been winched away from the Edda production platform. Minutes before 18:30 those on board felt a 'sharp crack' followed by 'some kind of trembling'. Suddenly the rig heeled over 30° and then stabilised. Five of the six anchor cables had broken, with one remaining cable preventing the rig from capsizing. The list continued to increase and at 18:53 the remaining anchor cable snapped and the rig turned upside down.
A year later in March 1981, the investigative report[40] concluded that the rig collapsed owing to a fatigue crack in one of its six bracings (bracing D-6), which connected the collapsed D-leg to the rest of the rig. This was traced to a small 6 mm fillet weld which joined a non-load-bearing flange plate to this D-6 bracing. This flange plate held a sonar device used during drilling operations. The poor profile of the fillet weld contributed to a reduction in its fatigue strength. Further, the investigation found considerable amounts of lamellar tearing in the flange plate and cold cracks in the butt weld. Cold cracks in the welds, increased stress concentrations due to the weakened flange plate, the poor weld profile, and cyclical stresses (which would be common in the North Sea), seemed to collectively play a role in the rig's collapse.
Others
- The 1862 Hartley Colliery Disaster was caused by the fracture of a steam engine beam and killed 220 people.
- The 1919 Boston Great Molasses Flood has been attributed to a fatigue failure.
- The 1948 Northwest Airlines Flight 421 crash due to fatigue failure in a wing spar root
- The 1957 "Mt. Pinatubo", presidential plane of Philippine President Ramon Magsaysay, crashed due to engine failure caused by metal fatigue.
- The 1965 capsize of the UK's first offshore oil platform, the Sea Gem, was due to fatigue in part of the suspension system linking the hull to the legs.
- The 1968 Los Angeles Airways Flight 417 lost one of its main rotor blades due to fatigue failure.
- The 1968 MacRobertson Miller Airlines Flight 1750 lost a wing due to improper maintenance leading to fatigue failure.
- The 1977 Dan-Air Boeing 707 crash caused by fatigue failure resulting in the loss of the right horizontal stabilizer.
- The 1980 LOT Flight 7 crashed due to fatigue in an engine turbine shaft resulting in engine disintegration leading to loss of control.
- The 1985 Japan Airlines Flight 123 crashed after the aircraft lost its vertical stabilizer due to faulty repairs on the rear bulkhead.
- The 1988 Aloha Airlines Flight 243 suffered an explosive decompression at 24,000 feet (7,300 m) after a fatigue failure.
- The 1989 United Airlines Flight 232 lost its tail engine due to fatigue failure in a fan disk hub.
- The 1992 El Al Flight 1862 lost both engines on its right-wing due to fatigue failure in the pylon mounting of the #3 Engine.
- The 1998 Eschede train disaster was caused by fatigue failure of a single composite wheel.
- The 2000 Hatfield rail crash was likely caused by rolling contact fatigue.
- The 2000 recall of 6.5 million Firestone tires on Ford Explorers originated from fatigue crack growth leading to separation of the tread from the tire.[41]
- The 2002 China Airlines Flight 611 disintegrated in-flight due to fatigue failure.
- The 2005 Chalk's Ocean Airways Flight 101 lost its right wing due to fatigue failure brought about by inadequate maintenance practices.
- The 2009 Viareggio train derailment due to fatigue failure.
- The 2009 Sayano–Shushenskaya power station accident due to metal fatigue of turbine mountings.
See also
- Aviation safety
- Embedment
- Forensic materials engineering
- Fractography
- Thermo-mechanical fatigue
- Critical plane analysis
- Vibration fatigue
- Solder Fatigue
References
^ Kim, W. H.; Laird, C. (1978). "Crack nucleation and stage I propagation in high strain fatigue—II. mechanism". Acta Metallurgica. 26 (5): 789–799. doi:10.1016/0001-6160(78)90029-9..mw-parser-output cite.citation{font-style:inherit}.mw-parser-output .citation q{quotes:"""""""'""'"}.mw-parser-output .citation .cs1-lock-free a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/6/65/Lock-green.svg/9px-Lock-green.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-limited a,.mw-parser-output .citation .cs1-lock-registration a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/d/d6/Lock-gray-alt-2.svg/9px-Lock-gray-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .citation .cs1-lock-subscription a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/a/aa/Lock-red-alt-2.svg/9px-Lock-red-alt-2.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration{color:#555}.mw-parser-output .cs1-subscription span,.mw-parser-output .cs1-registration span{border-bottom:1px dotted;cursor:help}.mw-parser-output .cs1-ws-icon a{background:url("//upload.wikimedia.org/wikipedia/commons/thumb/4/4c/Wikisource-logo.svg/12px-Wikisource-logo.svg.png")no-repeat;background-position:right .1em center}.mw-parser-output code.cs1-code{color:inherit;background:inherit;border:inherit;padding:inherit}.mw-parser-output .cs1-hidden-error{display:none;font-size:100%}.mw-parser-output .cs1-visible-error{font-size:100%}.mw-parser-output .cs1-maint{display:none;color:#33aa33;margin-left:0.3em}.mw-parser-output .cs1-subscription,.mw-parser-output .cs1-registration,.mw-parser-output .cs1-format{font-size:95%}.mw-parser-output .cs1-kern-left,.mw-parser-output .cs1-kern-wl-left{padding-left:0.2em}.mw-parser-output .cs1-kern-right,.mw-parser-output .cs1-kern-wl-right{padding-right:0.2em}
^ Stephens, R. I.; Fuchs, H. O. (2001). Metal Fatigue in Engineering (2nd ed.). John Wiley & Sons. p. 69. ISBN 978-0-471-51059-8.
^ Bathias, C. (1999). "There is no infinite fatigue life in metallic materials". Fatigue & Fracture of Engineering Materials & Structures. 22 (7): 559–565. doi:10.1046/j.1460-2695.1999.00183.x.
^ Shigley, J. E.; Mischke, C. R.; Budynas, R. G. (2003). Mechanical Engineering Design (7th ed.). McGraw Hill Higher Education. ISBN 978-0-07-252036-1.
^ Bäumel, A. Jr.; Seeger, T. (1990). Materials Data for Cyclic Loading, Supplement 1. Materials Science Monographs. 61. Elsevier. ISBN 978-0-444-88603-3.
^ Korkmaz, S. (2010). Uniform Material Law: Extension to High-Strength Steels. VDM. ISBN 978-3-639-25625-3.
^ Korkmaz, S. (2011). "A Methodology to Predict Fatigue Life of Cast Iron: Uniform Material Law for Cast Iron". International Journal of Iron and Steel Research. 18 (8): 42–45. doi:10.1016/S1006-706X(11)60102-7.
^ Fleck, N. A.; Shin, C. S.; Smith, R.A. (1985). "Fatigue Crack Growth Under Compressive Loading". Engineering Fracture Mechanics. 21 (1): 173–185. doi:10.1016/0013-7944(85)90063-3.
^ ab Schutz, W. (1996). "A history of fatigue". Engineering Fracture Mechanics. 54 (2): 263–300. doi:10.1016/0013-7944(95)00178-6.
^ Rankine, W. J. M. (1843). "On the causes of the unexpected breakage of the journals of railway axles, and on the means of preventing such accidents by observing the law of continuity in their construction". Minutes of the Proceedings of the Institution of Civil Engineers. 2 (1843): 105–107. doi:10.1680/imotp.1843.24600.
^ Braithwaite, F. (1854). "On the fatigue and consequent fracture of metals". Institution of Civil Engineers, Minutes of Proceedings. 13 (1854): 463–467. doi:10.1680/imotp.1854.23960.
^ Basquin, O. H. (1910). "The exponential law of endurance test". Proceedings of the American Society for Testing and Materials. 10: 625–630.
^ Cadwell, Sidney; Merrill; Sloman; Yost (1940). "Dynamic fatigue life of rubber". Rubber Chemistry and Technology. 13 (2): 304–315. doi:10.5254/1.3539515.
^ Murray, W. M., ed. (1952). "The statistical aspect of fatigue failure and its consequences". Fatigue and Fracture of Metals. Technology Press of the Massachusetts Institute of Technology/Wiley. pp. 182–196.
^ Matsuishi, M.; Endo, T. (1968). Fatigue of Metals Subjected to Varying Stress. Japan Society of Mechanical Engineers.
^ Brown, M. W.; Miller, K. J. (1973). "A theory for fatigue failure under multiaxial stress-strain conditions". Proceedings of the Institution of Mechanical Engineers. 187 (1): 745–755. doi:10.1243/PIME_PROC_1973_187_161_02.
^ Burhan, Ibrahim; Kim, Ho Sun (September 2018). "S-N Curve Models for Composite Materials Characterisation: An Evaluative Review". Journal of Composites Science. 2 (3): 38–66. doi:10.3390/jcs2030038.
^ Weibull, Waloddi (1961). Fatigue testing and analysis of results. Oxford: Published for Advisory Group for Aeronautical Research and development, North Atlantic Treaty Organization, by Pergamon Press. ISBN 978-0-08-009397-0. OCLC 596184290.
^ Kawai, M.; Itoh, N. (2014). "A failure-mode based anisomorphic constant life diagram for a unidirectional carbon/epoxy laminate under off-axis fatigue loading at room temperature". Journal of Composite Materials. 48 (5): 571–592. Bibcode:2014JCoMa..48..571K. CiteSeerX 10.1.1.826.6050. doi:10.1177/0021998313476324.
^ "The Rattle of Theta Chi (Stanford 1938)". 1942. Retrieved 26 November 2017.
^ Eskandari, H.; Kim, H. S. (2017). "A theory for mathematical framework and fatigue damage function for S-N plane". In Wei, Z.; Nikbin, K.; McKeighan, P. C.; Harlow, G. D. Fatigue and Fracture Test Planning, Test Data Acquisitions and Analysis. ASTM Selected Technical Papers. 1598. pp. 299–336. doi:10.1520/STP159820150099. ISBN 978-0-8031-7639-3.
^ Kim, H. S. (2016). Mechanics of Solids and Fracture (2nd ed.). Ventus Publishing. ISBN 978-87-403-1395-6.
^ Beardmore, R. (13 January 2013). "Fatigue Stress Action Types". Roymechx.
^ Paris, P. C.; Gomez, M. P.; Anderson, W. E. (1961). "A rational analytic theory of fatigue" (PDF). The Trend in Engineering. 13: 9–14.
^ Kim, S. T.; Tadjiev, D.; Yang, H. T. (2006). "Fatigue Life Prediction under Random Loading Conditions in 7475-T7351 Aluminum Alloy using the RMS Model". International Journal of Damage Mechanics. 15 (1): 89–102. doi:10.1177/1056789506058605.
^ Courtney, T. H. (2005). Mechanical Behavior of Materials. Waveland Press. pp. 578–581. ISBN 978-1-57766-425-3.
^ Coffin, L. F. Jr. (1954). "A study of the effects of cyclic thermal stresses on a ductile metal". Transactions of the ASME. 76: 931–950.
^ Manson, S. S. (1953). "Behavior of materials under conditions of thermal stress" (PDF). National Advisory Committee for Aeronautics. NACA TN-2933.
^ O'Donnell, W. J.; Langer, B. F. (1964). "Fatigue Design Basis for Zircaloy Components". Nuclear Science and Engineering. 20 (1): 1–12. doi:10.13182/NSE64-A19269.
^ Lawrence, F.V. (2015). "Mechanisms of Fatigue Crack Initiation and Growth" (PDF). University of Illinois. Retrieved 2017-12-11.
^ Murakami, Y.; Yokoyama, N. N.; Nagata, J. (2002-09-01). "Mechanism of fatigue failure in ultralong life regime". Fatigue & Fracture of Engineering Materials & Structures. 25 (8–9): 735–746. doi:10.1046/j.1460-2695.2002.00576.x. ISSN 1460-2695.
^ Udomphol, T. (2007). "Fatigue of metals" (PDF). Suranaree University of Technology. p. 54. Archived from the original (PDF) on 2013-01-02. Retrieved 2013-01-26.
^ "Material Technologies, Inc. Completes EFS Inspection of Bridge in New Jersey" (Press release). Material Technologies. 17 April 2007.
^ Hoffer, W. (June 1989). "Horrors in the Skies". Popular Mechanics. 166 (6): 67–70, 115–117.
^ Can Yildirim, H.; Marquis, G. B. (2012). "Fatigue strength improvement factors for high strength steel welded joints treated by high frequency mechanical impact". International Journal of Fatigue. 44: 168–176. doi:10.1016/j.ijfatigue.2012.05.002.
^ Can Yildirim, H.; Marquis, G. B.; Barsoum, Z. (2013). "Fatigue assessment of High Frequency Mechanical Impact (HFMI)-improved fillet welds by local approaches". International Journal of Fatigue. 52: 57–67. doi:10.1016/j.ijfatigue.2013.02.014.
^ "Research (Laser Peening)". LAMPL.
^ "Search Results for 'fatigue'". Cryogenic Treatment Database.
^ "ObjectWiki: Fuselage of de Havilland Comet Airliner G-ALYP". Science Museum. 24 September 2009. Archived from the original on 7 January 2009. Retrieved 9 October 2009.
^ The Alexander L. Kielland accident, Report of a Norwegian public commission appointed by royal decree of March 28, 1980, presented to the Ministry of Justice and Police March. Norwegian Public Reports 1981:11. Norwegian Ministry of Justice and Public Security. 1981. ASIN B0000ED27N.
^ Ansberry, C. (5 February 2001). "In Firestone Tire Study, Expert Finds Vehicle Weight Was Key in Failure". Wall Street Journal. Retrieved 6 September 2016.
Further reading
PDL Staff (1995). Fatigue and Tribological Properties of Plastics and Elastomers. Plastics Design Library. ISBN 978-1-884207-15-0.
Leary, M.; Burvill, C. (2009). "Applicability of published data for fatigue-limited design". Quality and Reliability Engineering International. 25 (8): 921–932. doi:10.1002/qre.1010.
Dieter, G. E. (2013). Mechanical Metallurgy. McGraw-Hill. ISBN 978-1259064791.
Little, R.E.; Jebe, E.H. (1975). Statistical Design of Fatigue Experiments. John Wiley & Sons. ISBN 978-0-470-54115-9.
Palmgren, A. G. (1924). "Die Lebensdauer von Kugellagern" [Life Length of Roller Bearings]. Zeitschrift des Vereines Deutscher Ingenieure (in German). 68 (14): 339–341.
Schijve, J. (2009). Fatigue of Structures and Materials. Springer. ISBN 978-1-4020-6807-2.
Lalanne, C. (2009). Fatigue Damage. ISTE - Wiley. ISBN 978-1-84821-125-4.
Pook, L. (2007). Metal Fatigue, What it is, Why it matters. Springer. ISBN 978-1-4020-5596-6.
Draper, J. (2008). Modern Metal Fatigue Analysis. EMAS. ISBN 978-0-947817-79-4.
Suresh, S. (2004). Fatigue of Materials. Cambridge University Press. ISBN 978-0-521-57046-6.
Kim, H. S. (2018). Mechanics of Solids and Fracture, 3rd ed. Bookboon, London. ISBN 978-87-403-2393-1.
External links
| Wikimedia Commons has media related to Material fatigue. |
- Fatigue by Shawn M. Kelly
- SAE Fatigue, Design, and Evaluation Committee website
- Article regarding Fatigue Testing of Bolted Joints
- Examples of fatigued metal products
- A collection of fatigue knowledge and calculators
- MATDAT.COM - Material Properties Database - Monotonic, Cyclic and Fatigue Properties of Steels, Aluminum and Titanium Alloys
- Application note on fatigue crack propagation in UHMWPE
- Video on the fatigue test, Karlsruhe University of Applied Sciences
- Introduction to the fundamentals of durability engineering


