Egftnjytyk

CIELAB color space top view

CIELAB color space front view

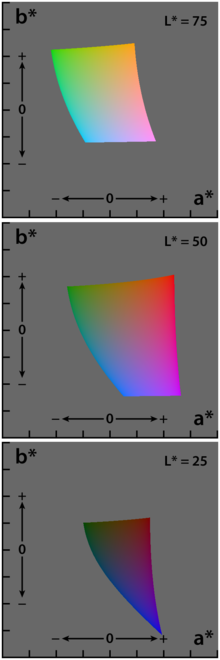
The CIE 1976 (L*, a*, b*) color space (CIELAB), showing only colors that fit within the sRGB gamut (and can therefore be displayed on a typical computer display). Each axis of each square ranges from −128 to 128.

The CIELAB color space (also known as CIE L*a*b* or sometimes abbreviated as simply "Lab" color space) is a color space defined by the International Commission on Illumination (CIE) in 1976. It expresses color as three numerical values, L* for the lightness and a* and b* for the green–red and blue–yellow color components. CIELAB was designed to be perceptually uniform with respect to human color vision, meaning that the same amount of numerical change in these values corresponds to about the same amount of visually perceived change.

With respect to a given white point, the CIELAB model is device-independent—it defines colors independently of how they are created or displayed. The CIELAB color space is typically used when graphics for print have to be converted from RGB to CMYK, as the CIELAB gamut includes both the gamuts of the RGB and CMYK color models.

The space itself is a three-dimensional real number space, allowing an infinite number of possible representations of colors. In practice, the space is usually mapped onto a three-dimensional integer space for digital representation, and thus the L*, a*, and b* values are usually absolute, with a pre-defined range. The lightness value, L*, represents the darkest black at L* = 0, and the brightest white at L* = 100. The color channels, a* and b*, represent true neutral gray values at a* = 0 and b* = 0. The a* axis represents the green–red component, with green in the negative direction and red in the positive direction. The b* axis represents the blue–yellow component, with blue in the negative direction and yellow in the positive direction. The scaling and limits of the a* and b* axes will depend on the specific implementation, as described below, but they often run in the range of ±100 or −128 to +127 (signed 8-bit integer).

The CIELAB color space was derived from the prior "master" CIE 1931 XYZ color space, which predicts which spectral power distributions will be perceived as the same color (see metamerism), but is not particularly perceptually uniform.^[1] Strongly influenced by the Munsell color system, the intention behind CIELAB was to create a space that can be computed via simple formulas from the CIEXYZ space but is more perceptually uniform than CIEXYZ.^[2] When storing color values using limited precision, using a perceptually uniform color space can improve the reproduction of tones.

CIELAB colors are defined relative to the white point of the CIEXYZ space from which they were converted; thus CIELAB values do not define absolute colors unless the white point is also specified. Often, in practice, the white point is assumed to follow a standard and is not explicitly stated (e.g., for "absolute colorimetric" rendering intent, the International Color Consortium L*a*b* values are relative to CIE standard illuminant D50, while they are relative to the unprinted substrate for other rendering intents).^[3]

The lightness correlate in CIELAB is calculated using the cube root of the relative luminance.

Advantages

An example of color enhancement using LAB color mode in Photoshop. The left side of the photo is enhanced, while the right side is normal.

Unlike the RGB and CMYK color models, Lab color is designed to approximate human vision. It aspires to perceptual uniformity, and its L component closely matches human perception of lightness, although it does not take the Helmholtz–Kohlrausch effect into account. Thus, it can be used to make accurate color balance corrections by modifying output curves in the a and b components, or to adjust the lightness contrast using the L component. In RGB or CMYK spaces, which model the output of physical devices rather than human visual perception, these transformations can be done only with the help of appropriate blend modes in the editing application.

Because the Lab space is larger than the gamut of computer displays and printers and because the visual stepwidths are relatively different to the color area, a bitmap image represented as Lab requires more data per pixel to obtain the same precision as an RGB or CMYK bitmap. In the 1990s, when computer hardware and software were limited to storing and manipulating mostly 8-bit/channel bitmaps, converting an RGB image to Lab and back was a very lossy operation. With 16-bit/channel and floating-point support now common, the loss due to quantization is negligible.

CIELAB is copyright and licence-free: as it is fully mathematically defined, the CIELAB model is public domain, it is in all respects freely usable and integrable (also systematic Lab / HLC color value tables).

A big portion of the Lab coordinate space cannot be generated by spectral distributions, it therefore falls outside the human vision and such Lab values are not "colors".

Differentiation

Some specific uses of the abbreviation in software, literature etc.

• In Adobe Photoshop, image editing using "Lab mode" is CIELAB D50.^[4][5]
  


• In Affinity Photo, Lab editing is achieved by changing the document's Colour Format to "Lab (16 bit)"


• In ICC profiles, the "Lab color space" used as a profile connection space is CIELAB D50.^[3]
  


• In TIFF files, the CIELAB color space may be used.^[6]
  


• In PDF documents, the "Lab color space" is CIELAB.^[7][8]
  


• In Digital Color Meter on macOS, it is described as "L*a*b*"


• In the open source non-destructive-editing software RawTherapee, the "Lab color space" is CIELAB.^[9]
  

CIELAB

Play media

Play media

The sRGB gamut (left) and visible gamut under D65 illumination (right) plotted within the CIELAB color space. a and b are the horizontal axes; L is the vertical axis.

CIE L*a*b* (CIELAB) is a color space specified by the International Commission on Illumination (French Commission internationale de l'éclairage, hence its CIE initialism). It describes all the colors visible to the human eye and was created to serve as a device-independent model to be used as a reference.

The three coordinates of CIELAB represent the lightness of the color (L* = 0 yields black and L* = 100 indicates diffuse white; specular white may be higher), its position between red/magenta and green (a*, negative values indicate green while positive values indicate magenta) and its position between yellow and blue (b*, negative values indicate blue and positive values indicate yellow). The asterisk (*) after L, a and b are pronounced star and are part of the full name, since they represent L*, a* and b*, to distinguish them from Hunter's L, a, and b, described below.

Since the L*a*b* model is a three-dimensional model, it can be represented properly only in a three-dimensional space.^[10] Two-dimensional depictions include chromaticity diagrams: sections of the color solid with a fixed lightness. It is crucial to realize that the visual representations of the full gamut of colors in this model are never accurate; they are there just to help in understanding the concept.

Because the red-green and yellow-blue opponent channels are computed as differences of lightness transformations of (putative) cone responses, CIELAB is a chromatic value color space.

A related color space, the CIE 1976 (L*, u*, v*) color space (a.k.a. CIELUV), preserves the same L* as L*a*b* but has a different representation of the chromaticity components. CIELAB and CIELUV can also be expressed in cylindrical form (CIELCH^[11] and CIELCH_uv, respectively), with the chromaticity components replaced by correlates of chroma and hue.

Since CIELAB and CIELUV, the CIE has been incorporating an increasing number of color appearance phenomena into their models, to better model color vision. These color appearance models, of which CIELAB is a simple example,^[12] culminated with CIECAM02.

Perceptual differences

This topic is covered in more detail at Color difference.

The nonlinear relations for L*, a*, and b* are intended to mimic the nonlinear response of the eye. Furthermore, uniform changes of components in the L*a*b* color space aim to correspond to uniform changes in perceived color, so the relative perceptual differences between any two colors in L*a*b* can be approximated by treating each color as a point in a three-dimensional space (with three components: L*, a*, b*) and taking the Euclidean distance between them.^[13]

RGB and CMYK conversions

There are no simple formulas for conversion between RGB or CMYK values and L*a*b*, because the RGB and CMYK color models are device-dependent. The RGB or CMYK values first must be transformed to a specific absolute color space, such as sRGB or Adobe RGB. This adjustment will be device-dependent, but the resulting data from the transform will be device-independent, allowing data to be transformed to the CIE 1931 color space and then transformed into L*a*b*.

Range of coordinates

As mentioned previously, the L* coordinate ranges from 0 to 100. The possible range of a* and b* coordinates is independent of the color space that one is converting from, since the conversion below uses X and Y, which come from RGB.

CIELAB–CIEXYZ conversions

Forward transformation

L⋆=116 f(YYn)−16a⋆=500(f(XXn)−f(YYn))b⋆=200(f(YYn)−f(ZZn)){displaystyle {begin{aligned}L^{star }&=116 f!left({frac {Y}{Y_{mathrm {n} }}}right)-16\a^{star }&=500left(f!left({frac {X}{X_{mathrm {n} }}}right)-f!left({frac {Y}{Y_{mathrm {n} }}}right)right)\b^{star }&=200left(f!left({frac {Y}{Y_{mathrm {n} }}}right)-f!left({frac {Z}{Z_{mathrm {n} }}}right)right)end{aligned}}}

where

f(t)={t3if t>δ3t3δ2+429otherwiseδ=629{displaystyle {begin{aligned}f(t)&={begin{cases}{sqrt[{3}]{t}}&{text{if }}t>delta ^{3}\{frac {t}{3delta ^{2}}}+{frac {4}{29}}&{text{otherwise}}end{cases}}\delta &={frac {6}{29}}end{aligned}}}

Here, X_n, Y_n and Z_n are the CIE XYZ tristimulus values of the reference white point (the subscript n suggests "normalized").

Under Illuminant D65 with normalization Y = 100, the values are

Xn=95.047,Yn=100.000,Zn=108.883{displaystyle {begin{aligned}X_{mathrm {n} }&=95.047,\Y_{mathrm {n} }&=100.000,\Z_{mathrm {n} }&=108.883end{aligned}}}

Values for illuminant D50 are

Xn=96.6797,Yn=100.000,Zn=82.5188{displaystyle {begin{aligned}X_{mathrm {n} }&=96.6797,\Y_{mathrm {n} }&=100.000,\Z_{mathrm {n} }&=82.5188end{aligned}}}

The division of the domain of the f function into two parts was done to prevent an infinite slope at t = 0. The function f was assumed to be linear below some t = t₀, and was assumed to match the t^1/3 part of the function at t₀ in both value and slope. In other words:

t01/3=mt0+c (match in value)13t0−2/3=m (match in slope){displaystyle {begin{aligned}t_{0}^{1/3}&=mt_{0}+c&{text{ (match in value)}}\{frac {1}{3}}t_{0}^{-2/3}&=m&{text{ (match in slope)}}end{aligned}}}

The intercept f(0) = c was chosen so that L* would be 0 for Y = 0: c = 16/116 = 4/29. The above two equations can be solved for m and t₀:

m=13δ−2=7.787037…t0=δ3=0.008856…{displaystyle {begin{aligned}m&={frac {1}{3}}delta ^{-2}&=7.787037ldots \t_{0}&=delta ^{3}&=0.008856ldots end{aligned}}}

where δ = 6/29.^[14]

Reverse transformation

The reverse transformation is most easily expressed using the inverse of the function f above:

X=Xnf−1(L⋆+16116+a⋆500)Y=Ynf−1(L⋆+16116)Z=Znf−1(L⋆+16116−b⋆200){displaystyle {begin{aligned}X&=X_{mathrm {n} }f^{-1}left({frac {L^{star }+16}{116}}+{frac {a^{star }}{500}}right)\Y&=Y_{mathrm {n} }f^{-1}left({frac {L^{star }+16}{116}}right)\Z&=Z_{mathrm {n} }f^{-1}left({frac {L^{star }+16}{116}}-{frac {b^{star }}{200}}right)\end{aligned}}}

where

f−1(t)={t3if t>δ3δ2(t−429)otherwise{displaystyle f^{-1}(t)={begin{cases}t^{3}&{text{if }}t>delta \3delta ^{2}left(t-{frac {4}{29}}right)&{text{otherwise}}end{cases}}}

and where δ = 6/29.

Hunter Lab

The Hunter Lab color space, defined in 1948^[15][16] by Richard S. Hunter, is another color space sometimes referred to as "Lab". Like CIELAB, it was also designed to be computed via simple formulas from the CIEXYZ space but to be more perceptually uniform than CIEXYZ. Hunter named his coordinates L, a, and b; the CIELAB space, defined years later in 1976, named its coordinates L*, a*, and b* to distinguish them from Hunter's coordinates.

L is a correlate of lightness, and is computed from the Y tristimulus value using Priest's approximation to Munsell value:

L=100Y/Yn{displaystyle L=100{sqrt {Y/Y_{mathrm {n} }}}}

where Y_n is the Y tristimulus value of a specified white object. For surface-color applications, the specified white object is usually (though not always) a hypothetical material with unit reflectance that follows Lambert's law. The resulting L will be scaled between 0 (black) and 100 (white); roughly ten times the Munsell value. Note that a medium lightness of 50 is produced by a luminance of 25, since 10025/100=100⋅1/2{displaystyle 100{sqrt {25/100}}=100cdot 1/2}

a and b are termed opponent color axes. a represents, roughly, Redness (positive) versus Greenness (negative). It is computed as:

a=Ka(X/Xn−Y/YnY/Yn){displaystyle a=K_{mathrm {a} }left({frac {X/X_{mathrm {n} }-Y/Y_{mathrm {n} }}{sqrt {Y/Y_{mathrm {n} }}}}right)}

where K_a is a coefficient that depends upon the illuminant (for D65, K_a is 172.30; see approximate formula below) and X_n is the X tristimulus value of the specified white object.

The other opponent color axis, b, is positive for yellow colors and negative for blue colors. It is computed as:

b=Kb(Y/Yn−Z/ZnY/Yn){displaystyle b=K_{mathrm {b} }left({frac {Y/Y_{mathrm {n} }-Z/Z_{mathrm {n} }}{sqrt {Y/Y_{mathrm {n} }}}}right)}

where K_b is a coefficient that depends upon the illuminant (for D65, K_b is 67.20; see approximate formula below) and Z_n is the Z tristimulus value of the specified white object.^[17]

Both a and b will be zero for objects that have the same chromaticity coordinates as the specified white objects (i.e., achromatic, grey, objects).

Approximate formulas for K_a and K_b

In the previous version of the Hunter Lab color space, K_a was 175 and K_b was 70. Hunter Associates Lab discovered^{[citation needed]} that better agreement could be obtained with other color difference metrics, such as CIELAB (see above) by allowing these coefficients to depend upon the illuminants. Approximate formulae are:

Ka≈175198.04(Xn+Yn){displaystyle K_{mathrm {a} }approx {frac {175}{198.04}}(X_{mathrm {n} }+Y_{mathrm {n} })}

Kb≈70218.11(Yn+Zn){displaystyle K_{mathrm {b} }approx {frac {70}{218.11}}(Y_{mathrm {n} }+Z_{mathrm {n} })}

which result in the original values for Illuminant C, the original illuminant with which the Lab color space was used.

As an Adams chromatic valence space

Adams chromatic valence color spaces are based on two elements: a (relatively) uniform lightness scale, and a (relatively) uniform chromaticity scale.^[18] If we take as the uniform lightness scale Priest's approximation to the Munsell Value scale, which would be written in modern notation:

L=100Y/Yn{displaystyle L=100{sqrt {Y/Y_{mathrm {n} }}}}

and, as the uniform chromaticity coordinates:

ca=X/XnY/Yn−1=X/Xn−Y/YnY/Yn{displaystyle c_{mathrm {a} }={frac {X/X_{mathrm {n} }}{Y/Y_{mathrm {n} }}}-1={frac {X/X_{mathrm {n} }-Y/Y_{mathrm {n} }}{Y/Y_{mathrm {n} }}}}

cb=ke(1−Z/ZnY/Yn)=keY/Yn−Z/ZnY/Yn{displaystyle c_{mathrm {b} }=k_{mathrm {e} }left(1-{frac {Z/Z_{mathrm {n} }}{Y/Y_{mathrm {n} }}}right)=k_{mathrm {e} }{frac {Y/Y_{mathrm {n} }-Z/Z_{mathrm {n} }}{Y/Y_{mathrm {n} }}}}

where k_e is a tuning coefficient, we obtain the two chromatic axes:

a=K⋅L⋅ca=K⋅100X/Xn−Y/YnY/Yn{displaystyle a=Kcdot Lcdot c_{mathrm {a} }=Kcdot 100{frac {X/X_{mathrm {n} }-Y/Y_{mathrm {n} }}{sqrt {Y/Y_{mathrm {n} }}}}}

and

b=K⋅L⋅cb=K⋅100keY/Yn−Z/ZnY/Yn{displaystyle b=Kcdot Lcdot c_{mathrm {b} }=Kcdot 100k_{mathrm {e} }{frac {Y/Y_{mathrm {n} }-Z/Z_{mathrm {n} }}{sqrt {Y/Y_{mathrm {n} }}}}}

which is identical to the Hunter Lab formulas given above if we select K = K_a/100 and k_e = K_b/K_a. Therefore, the Hunter Lab color space is an Adams chromatic valence color space.

Cylindrical representation: CIELCh or CIEHLC

Play media

Play media

The sRGB gamut (left) and visible gamut under D65 illumination (right) plotted within the CIELCHab color space. L is the vertical axis; C is the cylinder radius; h is the angle around the circumference.

The CIELCh color space is a CIELab cube color space, where instead of Cartesian coordinates a*, b*, the cylindrical coordinates C* (chroma, relative saturation) and h° (hue angle, angle of the hue in the CIELab color wheel) are specified. The CIELab lightness L* remains unchanged.

The conversion of a* and b* to C* and h° is done using the following formulas:

C⋆=a⋆2+b⋆2,h∘=arctan⁡(b⋆a⋆){displaystyle C^{star }={sqrt {a^{star ,2}+b^{star ,2}}},qquad h^{circ }=arctan left({frac {b^{star }}{a^{star }}}right)}

Conversely, given the polar coordinates, conversion to Cartesian coordinates is achieved with:

a⋆=C⋆cos⁡(h∘),b⋆=C⋆sin⁡(h∘){displaystyle a^{star }=C^{star }cos(h^{circ }),qquad b^{star }=C^{star }sin(h^{circ })}

The LCh color space is not the same as the HSV, HSL or HSB color models, although their values can also be interpreted as a base color, saturation and lightness of a color. The HSL values are a polar coordinate transformation of what is technically defined RGB cube color space. LCh is still perceptually uniform.

Further, H and h are not identical, because HSL space uses as primary colors the three additive primary colors red, green, blue (H = 0, 120, 240°). Instead, the LCh system uses the four colors yellow, green, blue and red (h = 90, 180, 270, 360°). Regardless the angle h, C = 0 means the achromatic colors, that is, the gray axis.

The simplified spellings LCh, LCH and HLC are common, but the latter presents a different order. HCL color space (Hue-Chroma-Luminance) on the other hand is a commonly used alternative name for the L*C*h(uv) color space, also known as the cylindrical representation or polar CIELUV.

See also

• Color theory


• Opponent color theory


• HSL and HSV


• RGB color model


• CMYK color model


• CIECAM02


• HCL color space

References

External links

• 
  Colorlab MATLAB toolbox for color science computation and accurate color reproduction (by Jesus Malo and Maria Jose Luque, Universitat de Valencia). It includes CIE standard tristimulus colorimetry and transformations to a number of non-linear color appearance models (CIE Lab, CIE CAM, etc.).


• Demonstrative color conversion applet


• 
  CIELAB Color Space by Gernot Hoffmann, includes explanations of L*a*b* conversion formulae, graphical depictions of various gamuts plotted in L*a*b* space, and PostScript code for performing the color transformations.


• Color Differences


• LAB Color Spaces with MATLAB


• Convert Rgb to Lab