Egftnjytyk

An illustration of how position angle is estimated through a telescope eyepiece; the primary star is at center.

Position angle, usually abbreviated PA, is the convention for measuring angles on the sky in astronomy. The International Astronomical Union defines it as the angle measured relative to the north celestial pole (NCP), turning positive into the direction of the right ascension. In the standard (non-flipped) images this is a counterclockwise measure relative to the axis into the direction of positive declination.

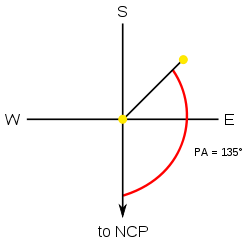
In the case of observed visual binary stars, it is defined as the angular offset of the secondary star from the primary relative to the north celestial pole.

As the example illustrates, if one were observing a hypothetical binary star with a PA of 135 degrees, that means an imaginary line in the eyepiece drawn from the north celestial pole to the primary (P) would be offset from the secondary (S) such that the NCP-P-S angle would be 135 degrees.

When graphing visual binary orbits, the NCP line is traditionally drawn downward—that is, with north at bottom—and PA is measured counterclockwise.

Also the direction of the proper motion can for example be given by its position angle.

The definition of position angle is also applied to extended objects like galaxies, where it refers to the angle made by the major axis of the object with the NCP line.

Nautics

The concept of the position angle is inherited from nautical navigation on the oceans, where the optimum compass course is the course from a known position $s$ to a target position $t$ with minimum effort. Setting aside the influence of winds and ocean currents, the optimum course is the course of smallest distance between the two positions on the ocean surface. Computing the compass course is known as the inverse problem of geodesics.

This article considers only the abstraction of minimizing the distance between $s$ and $t$ traveling on the surface of a sphere with some radius $R$ . In which direction angle $p$ relative to North should the ship steer to reach the target position?

Global geocentric coordinate system

The position angle of the point t at the point s is the angle at which the green and the dashed great circles intersect at s. The unit directions

u E

,

u N

and the rotation axis

ω

are marked by arrows.

Detailed evaluation of the optimum direction is possible if the sea surface is approximated by a sphere surface. The standard computation places the ship at a geodetic latitude $φ s$ and geodetic longitude $λ s$ , where $φ$ is considered positive if north of the equator, and where $λ$ is considered positive if east of Greenwich. In the global coordinate system centered at the center of the sphere, the Cartesian components are

{displaystyle {mathbf {s} }=Rleft({begin{array}{c}cos varphi _{s}cos lambda _{s}\cos varphi _{s}sin lambda _{s}\sin varphi _{s}end{array}}right)}

and the target position is

{displaystyle {mathbf {t} }=Rleft({begin{array}{c}cos varphi _{t}cos lambda _{t}\cos varphi _{t}sin lambda _{t}\sin varphi _{t}end{array}}right).}

The North Pole is at

{displaystyle {mathbf {N} }=Rleft({begin{array}{c}0\0\1end{array}}right).}

The minimum distance $d$ is the distance along a great circle that runs through $s$ and $t$ . It is calculated in a plane that contains the sphere center and the great circle,

{displaystyle d_{s,t}=Rtheta _{s,t}}

where $θ$ is the angular distance of two points viewed from the center of the sphere, measured in radians. The cosine of the angle is calculated by the dot product of the two vectors

{displaystyle mathbf {s} cdot mathbf {t} =R^{2}cos theta _{s,t}=R^{2}(sin varphi _{s}sin varphi _{t}+cos varphi _{s}cos varphi _{t}cos(lambda _{t}-lambda _{s}))}

If the ship steers straight to the North Pole, the travel distance is

{displaystyle d_{s,N}=Rtheta _{s,N}=R(pi /2-varphi _{s})}

If a ship starts at $t$ and swims straight to the North Pole, the travel distance is

{displaystyle d_{t,N}=Rtheta _{t,n}=R(pi /2-varphi _{t})}

Brief Derivation

The cosine formula of spherical trigonometry ^[1] yields for the
angle $p$ between the great circles through $s$ that point to the North on one hand and to $t$ on the other hand

{displaystyle cos theta _{t,N}=cos theta _{s,t}cos theta _{s,N}+sin theta _{s,t}sin theta _{s,N}cos p.}

{displaystyle sin varphi _{t}=cos theta _{s,t}sin varphi _{s}+sin theta _{s,t}cos varphi _{s}cos p.}

The sine formula yields

{displaystyle {frac {sin p}{sin theta _{t,N}}}={frac {sin(lambda _{t}-lambda _{s})}{sin theta _{s,t}}}.}

Solving this for $sin θ s,t$ and insertion in the previous formula gives an expression for the tangent of the position angle,

{displaystyle sin varphi _{t}=cos theta _{s,t}sin varphi _{s}+{frac {sin(lambda _{t}-lambda _{s})}{sin p}}cos varphi _{t}cos varphi _{s}cos p;}

{displaystyle tan p={frac {sin(lambda _{t}-lambda _{s})cos varphi _{t}cos varphi _{s}}{sin varphi _{t}-cos theta _{s,t}sin varphi _{s}}}.}

Long Derivation

Because the brief derivation gives an angle between 0 and $π$ which does not reveal the sign (west or east of north ?), a more explicit derivation is desirable which yields separately the sine and the cosine of $p$ such that use of the correct branch of the inverse tangent allows to produce an angle in the full range $-π\leqp\leqπ$ .

The computation starts from a construction of the great circle between $s$ and $t$ . It lies in the plane that contains the sphere center, $s$ and $t$ and is constructed rotating $s$ by the angle $θ s,t$ around an axis $ω$ . The axis is perpendicular to the plane of the great circle and computed by the normalized vector cross product of the two positions:

{displaystyle mathbf {omega } ={frac {1}{R^{2}sin theta _{s,t}}}mathbf {s} times mathbf {t} ={frac {1}{sin theta _{s,t}}}left({begin{array}{c}cos varphi _{s}sin lambda _{s}sin varphi _{t}-sin varphi _{s}cos varphi _{t}sin lambda _{t}\sin varphi _{s}cos lambda _{t}cos varphi _{t}-cos varphi _{s}sin varphi _{t}cos lambda _{s}\cos varphi _{s}cos varphi _{t}sin(lambda _{t}-lambda _{s})end{array}}right).}

A right-handed tilted coordinate system with the center at the center of the sphere is given by the
following three axes: the
axis $s$ , the axis

{displaystyle mathbf {s} _{perp }=omega times {frac {1}{R}}mathbf {s} ={frac {1}{sin theta _{s,t}}}left({begin{array}{c}cos varphi _{t}cos lambda _{t}(sin ^{2}varphi _{s}+cos ^{2}varphi _{s}sin ^{2}lambda _{s})-cos lambda _{s}(sin varphi _{s}cos varphi _{s}sin varphi _{t}+cos ^{2}varphi _{s}sin lambda _{s}cos varphi _{t}sin lambda _{t})\cos varphi _{t}sin lambda _{t}(sin ^{2}varphi _{s}+cos ^{2}varphi _{s}cos ^{2}lambda _{s})-sin lambda _{s}(sin varphi _{s}cos varphi _{s}sin varphi _{t}+cos ^{2}varphi _{s}cos lambda _{s}cos varphi _{t}cos lambda _{t})\cos varphi _{s}[cos varphi _{s}sin varphi _{t}-sin varphi _{s}cos varphi _{t}cos(lambda _{t}-lambda _{s})]end{array}}right)}

and the axis $ω$ .
A position along the great circle is

{displaystyle mathbf {s} (theta )=cos theta mathbf {s} +sin theta mathbf {s} _{perp },quad 0leq theta leq 2pi .}

The compass direction is given by inserting the two vectors $s$ and $s ⊥$ and computing the gradient of the vector with respect to $θ$ at $θ=0$ .

{displaystyle {frac {partial }{partial theta }}mathbf {s} _{mid theta =0}=mathbf {s} _{perp }.}

The angle $p$ is given by splitting this direction along two orthogonal directions in the plane tangential to the sphere at the point $s$ . The two directions are given by the partial derivatives of $s$ with respect to $φ$ and with respect to $λ$ , normalized to unit length:

{displaystyle mathbf {u} _{N}=left({begin{array}{c}-sin varphi _{s}cos lambda _{s}\-sin varphi _{s}sin lambda _{s}\cos varphi _{s}end{array}}right);}

{displaystyle mathbf {u} _{E}=left({begin{array}{c}-sin lambda _{s}\cos lambda _{s}\0end{array}}right);}

{displaystyle mathbf {u} _{N}cdot mathbf {s} =mathbf {u} _{E}cdot mathbf {u} _{N}=0}

$u N$ points north and $u E$ points east at the position $s$ .
The position angle $p$ projects $s ⊥$
into these two directions,

{displaystyle mathbf {s} _{perp }=cos p,mathbf {u} _{N}+sin p,mathbf {u} _{E}}

,

where the positive sign means the positive position angles are defined to be north over east. The values of the cosine and sine of $p$ are computed by multiplying this equation on both sides with the two unit vectors,

{displaystyle cos p=mathbf {s} _{perp }cdot mathbf {u} _{N}={frac {1}{sin theta _{s,t}}}[cos varphi _{s}sin varphi _{t}-sin varphi _{s}cos varphi _{t}cos(lambda _{t}-lambda _{s})];}

{displaystyle sin p=mathbf {s} _{perp }cdot mathbf {u} _{E}={frac {1}{sin theta _{s,t}}}[cos varphi _{t}sin(lambda _{t}-lambda _{s})].}

Instead of inserting the convoluted expression of $s ⊥$ , the evaluation may employ that the triple product is invariant under a circular shift
of the arguments:

{displaystyle cos p=(mathbf {omega } times {frac {1}{R}}mathbf {s} )cdot mathbf {u} _{N}=omega cdot ({frac {1}{R}}mathbf {s} times mathbf {u} _{N}).}

If atan2 is used to compute the value, one can reduce both expressions by division through $cos φ t$
and multiplication by $sin θ s,t$ ,
because these values are always positive and that operation does not change signs; then effectively

{displaystyle tan p={frac {sin(lambda _{t}-lambda _{s})}{cos varphi _{s}tan varphi _{t}-sin varphi _{s}cos(lambda _{t}-lambda _{s})}}.}

Astronomy

The parallactic angle of astronomy is the position angle of the zenith (considered the target position) as seen from the star (considered the starting position), where the North Celestial Pole (NCP) of the celestial sphere defines the reference direction.
The sign of the angle is basically kept, north over east in both cases,
but as astronomers look at stars from the inside of the celestial sphere,
the definition uses the convention that the $q$ is the angle in an image that turns the direction to the NCP counterclockwise into the direction of the zenith.

Brief Derivation

The formulas are special cases of the formulas shown above. In the equatorial system of right ascension $α$ and declination $δ$ of a star
one considers the spherical triangle with an angle $q$ at the position of the star,
with an angle $h$ , the hour angle, at the NCP, and with an angle $π-A$ at the
zenith, where $A$ is the azimuth in the south-over-west convention. The side lengths of the spherical triangle are (i) $π/2-φ$ as the distance from the zenith to the NCP, where $φ$ is the observer's geographic latitude, (ii) $π/2-δ$ as the distance between the star and the NCP, and (iii) $z=π/2-a$ , the zenith distance, complement to the star elevation, as the distance between the zenith and the star.

The cosine formula (one of the three cosine formulas) is

{displaystyle cos(pi /2-varphi )=cos(pi /2-delta )cos z+sin(pi /2-delta )sin zcos q.}

The sine formula is

{displaystyle {frac {sin |q|}{sin(pi /2-varphi )}}={frac {sin |h|}{sin z}}={frac {sin(pi -A)}{sin(pi /2-delta )}}.}

The 4-parts formula is

{displaystyle cos q=-cos hcos(pi -A)+sin |h|sin(pi -A)cos(pi /2-varphi ).}

As in the brief derivation above, these formulas hide the sign of $q$ and $h$ , which
we indicated by placing the absolute values in arguments of the sines, which are sign-dependent.

Long Derivation

The explicit vector algebra to recover the correct sign is equivalent to the calculation of the
long derivation for the compass course. In the global equatorial system the star is at

{displaystyle mathbf {s} =left({begin{array}{c}cos delta cos alpha \cos delta sin alpha \sin delta end{array}}right).}

In the same coordinate system the zenith is found by inserting $a=π/2$ , $cos a=0$
into the transformation formulas

{displaystyle mathbf {z} =left({begin{array}{c}cos varphi cos l\cos varphi sin l\sin varphi end{array}}right),}

where $φ$ is the observer's geographic latitude, $a$ the star's altitude,
$z=π/2-a$ the zenith distance, and $l$ the local sidereal time. The North Celestial Pole is at

{displaystyle mathbf {N} =left({begin{array}{c}0\0\1end{array}}right).}

The normalized cross product is the rotation axis that turns the star into the direction of the zenith:

{displaystyle mathbf {omega } _{z}={frac {1}{sin z}}mathbf {s} times mathbf {z} ={frac {1}{sin z}}left({begin{array}{c}cos delta sin alpha sin varphi -sin delta cos varphi sin l\-cos delta cos alpha sin varphi +sin delta cos varphi cos l\cos delta cos varphi sin(alpha -l)end{array}}right).}

Finally $ω z X s$ is the third axis of the tilted coordinate system and the direction into which the star is moved on the great circle towards the zenith.

The plane tangential to the celestial sphere at the star is spanned by the unit vectors to the north,

{displaystyle mathbf {u} _{delta }=left({begin{array}{c}-sin delta cos alpha \-sin delta sin alpha \cos delta end{array}}right),}

and to the east

{displaystyle mathbf {u} _{alpha }=left({begin{array}{c}-sin alpha \cos alpha \0end{array}}right).}

These are orthogonal:

{displaystyle mathbf {u} _{delta }cdot mathbf {u} _{alpha }=0;quad mathbf {u} _{delta }^{2}=mathbf {u} _{alpha }^{2}=1.}

The parallactic angle $q$ is the angle of the initial section of the great circle
at s, east of north,

{displaystyle omega _{z}times mathbf {s} =cos q,mathbf {u} _{delta }+sin q,mathbf {u} _{alpha }.}

{displaystyle cos q=(omega _{z}times mathbf {s} )cdot mathbf {u} _{delta }={frac {1}{sin z}}(cos delta sin varphi -sin delta cos varphi cos h),}

{displaystyle sin q=(omega _{z}times mathbf {s} )cdot mathbf {u} _{alpha }={frac {1}{sin z}}sin hcos varphi .}

The values of $sin z$ and of $cos φ$ are positive, so using atan2 functions one may
divide both expressions through these without losing signs; eventually

{displaystyle tan q={frac {sin hcos varphi }{cos delta sin varphi -sin delta cos varphi cos h}}={frac {sin h}{cos delta tan varphi -sin delta cos h}}}

yields the angle in the full range $-π \leq q \leq π$ . The advantage of this expression is that it
does not depend on the various offset conventions of $A$ ; the uncontroversial offset
of the hour angle $h$
takes care of this.

For a sidereal target, by definition a target where $δ$ and $α$ are not time-dependent,
the angle changes with a period of a sidereal day $T s$ .
Let dots denote time derivatives; then the hour angle changes as

{displaystyle {dot {h}}={frac {2pi }{T_{s}}}}

and the time derivative of the $tan q$ expression is

{displaystyle {dot {q}}{frac {1}{cos ^{2}q}}={frac {cos varphi [cos hcos delta sin varphi -sin delta cos varphi ]}{(cos delta sin varphi -sin delta cos varphi cos h)^{2}}}{dot {h}};}

{displaystyle {dot {q}}={frac {cos varphi [cos hcos delta sin varphi -sin delta cos varphi ]}{sin ^{2}z}}{dot {h}}={frac {cos varphi cos acos A}{sin ^{2}z}}{dot {h}}={frac {cos varphi cos A}{sin z}}{dot {h}}.}

References

^ Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 4.3.149". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.

External links

The Orbits of 150 Visual Binary Stars, by Dibon Smith (Accessed 2/26/06)

[AS-1] Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 4.3.149". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.

搜尋此網誌

Egftnjytyk

Position angle

Contents

Nautics

Global geocentric coordinate system

Brief Derivation

Long Derivation

Astronomy

Brief Derivation

Long Derivation

See also

Further reading

References

External links

這個網誌中的熱門文章

12.7 cm/40 Type 89 naval gun

Shark

Wiciokrzew