Elipsa







Ten artykuł dotyczy figury geometrycznej. Zobacz też: inne znaczenia tego słowa.



Elipsa otrzymana jako przecięcie stożka płaszczyzną.


Elipsa (gr. ἔλλειψις, elleipsis – „brak, opuszczenie, pominięcie”[1][2], zob. geneza) – przypadek ograniczonej krzywej stożkowej, czyli krzywej będącej częścią wspólną powierzchni stożkowej oraz przecinającej ją płaszczyzny. Jest to również miejsce geometryczne wszystkich tych punktów płaszczyzny, dla których suma odległości od dwóch ustalonych punktów jest stałą.


Elipsy powstają także jako obrazy okręgu lub sfery w rzucie równoległym i pewnych przypadkach rzutu perspektywicznego. W istocie okręgi są przypadkami szczególnymi elips. Elipsa jest również domkniętym i ograniczonym przypadkiem krzywej stopnia drugiego danej wzorem uwikłanym lub krzywej wymiernej drugiego stopnia. Jest to zarazem najprostsza figura Lissajous powstająca, gdy drgania poziome i pionowe mają tę samą częstotliwość.




Spis treści






  • 1 Podstawowe pojęcia i własności


    • 1.1 Półoś wielka, półoś mała, ogniska, kierownice


    • 1.2 Mimośród


    • 1.3 Spłaszczenie




  • 2 Geneza nazwy


  • 3 Kreślenie


    • 3.1 Metoda szpilek i sznurka


    • 3.2 Inne metody




  • 4 Geometria analityczna


  • 5 Własności


    • 5.1 Pole i obwód


    • 5.2 Styczna


    • 5.3 Dwie styczne


    • 5.4 Trójkąt opisany


    • 5.5 Okrąg opisany




  • 6 Uogólnienia


  • 7 Zobacz też


  • 8 Uwagi


  • 9 Przypisy


  • 10 Linki zewnętrzne





Podstawowe pojęcia i własności |




Elipsa


Elipsa to gładka krzywa zamknięta symetryczna względem jej środka. Odległość między punktami antypodycznymi elipsy, czyli parami punktów, których środek odcinka przez nie wyznaczany jest zarazem środkiem symetrii elipsy, jest maksymalna i minimalna wzdłuż dwóch prostopadłych kierunków – osi wielkiej (średnicy transwersalnej) oraz osi małej (średnicy sprzężonej).



Półoś wielka, półoś mała, ogniska, kierownice |


Półoś wielka i półoś mała elipsy (oznaczone na rysunku odpowiednio przez a{displaystyle a}a i b{displaystyle b}b) są połowami odpowiednio osi wielkiej i małej. Na osi wielkiej, po obu stronach jej środka, znajdują się dwa wyróżnione punkty F1{displaystyle F_{1}}F_1 oraz F2{displaystyle F_{2}}F_{2} takie, że suma odległości dowolnego punktu elipsy od wspomnianych punktów jest stała i równa długości osi wielkiej (2a).{displaystyle (2a).}{displaystyle (2a).} Każdy z tych dwóch punktów nazywany jest ogniskiem elipsy. Odległości ognisk od środka elipsy są równe:


c=a2−b2.{displaystyle c={sqrt {a^{2}-b^{2}}}.}{displaystyle c={sqrt {a^{2}-b^{2}}}.}

Jeżeli a{displaystyle a}a jest równe b,{displaystyle b,}b, to ogniska pokrywają się ze środkiem i wówczas elipsa staje się okręgiem o promieniu r=a=b.{displaystyle r=a=b.}{displaystyle r=a=b.}


Proste prostopadłe do półosi wielkiej elipsy, odległe od środka elipsy o:


d=a2c{displaystyle d={frac {a^{2}}{c}}}{displaystyle d={frac {a^{2}}{c}}}

są kierownicami elipsy. Dla okręgu (c=0){displaystyle (c=0)}{displaystyle (c=0)} kierownice znajdują się „w nieskończoności”.



Mimośród |


Mimośrodem (ekscentrycznością) elipsy nazywamy parametr e{displaystyle e}e będący wartością opisującą stosunek długości ogniskowej do długości półosi wielkiej.


Mimośród zawiera się w przedziale od 0 do 1. Jest on równy zeru wtedy i tylko wtedy, gdy a = b, a więc kiedy elipsa jest okręgiem. Gdy mimośród dąży do 1, elipsa wydłuża się, a współczynnik ab{displaystyle {tfrac {a}{b}}}{tfrac {a}{b}} dąży do nieskończoności.


Jeżeli elipsa o ogniskach F1=(−c,0){displaystyle F_{1}=(-c,0)}{displaystyle F_{1}=(-c,0)} i F2=(c,0){displaystyle F_{2}=(c,0)}{displaystyle F_{2}=(c,0)} jest dana równaniem analitycznym


x2a2+y2b2=1,{displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1,}{displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1,}

to


e=ca.{displaystyle e={frac {c}{a}}.}{displaystyle e={frac {c}{a}}.}

Odległość ae od ogniska do środka nazywana jest mimośrodem liniowym (ekscentrycznością liniową) elipsy.


W obliczeniach geodezyjnych i kartograficznych mają zastosowanie następujące oznaczenia[3]:


















mimośród
e{displaystyle e}e
e2=a2−b2a2{displaystyle e^{2}={frac {a^{2}-b^{2}}{a^{2}}}}{displaystyle e^{2}={frac {a^{2}-b^{2}}{a^{2}}}}
drugi mimośród
e′{displaystyle e'}e'
e′2=a2−b2b2{displaystyle {e'}^{2}={frac {a^{2}-b^{2}}{b^{2}}}}{displaystyle {e'}^{2}={frac {a^{2}-b^{2}}{b^{2}}}}  
trzeci mimośród
e″{displaystyle e''}{displaystyle e''}  
e″2=m=a−ba+b{displaystyle {e''}^{2}=m={frac {a-b}{a+b}}}{displaystyle {e''}^{2}=m={frac {a-b}{a+b}}}

Parametry te mają zastosowanie do elipsoidy obrotowej, ale wywodzą się z elipsy południkowej.



Spłaszczenie |


Podobnie w obliczeniach geodezyjnych i astronomicznych są używane parametry elipsy nazywane spłaszczeniem:


















(pierwsze) spłaszczenie
f=a−ba{displaystyle f={frac {a-b}{a}}}{displaystyle f={frac {a-b}{a}}}
 Podstawowe, odwrotność 1/f służy do określenia elipsoidy odniesienia.
drugie spłaszczenie
f′=a−bb{displaystyle f'={frac {a-b}{b}}}{displaystyle f'={frac {a-b}{b}}}
 Rzadziej używane.
trzecie spłaszczenie
n=f″=a−ba+b{displaystyle n=f''={frac {a-b}{a+b}}}{displaystyle n=f''={frac {a-b}{a+b}}}  
 Używane w obliczeniach geodezyjnych.


Geneza nazwy |


Nazwa „elipsa” została zaczerpnięta (według Pappusa z Aleksandrii) przez Apoloniusza z Pergi z wczesnej pitagorejskiej terminologii dotyczącej przykładania pól powierzchni: po przyłożeniu prostokąta do odcinka (tj. umieszczeniu podstawy prostokąta wzdłuż odcinka tak, by jeden z końców odcinka i jeden z końców podstawy pokrywały się) przyłożonemu prostokątowi „brakowało” do długości odcinka; równanie elipsy to y2=lx±b2x2/a2,{displaystyle y^{2}=lxpm b^{2}x^{2}/a^{2},}{displaystyle y^{2}=lxpm b^{2}x^{2}/a^{2},} gdzie l=b2/a,{displaystyle l=b^{2}/a,}{displaystyle l=b^{2}/a,} skąd y2<lx,{displaystyle y^{2}<lx,}{displaystyle y^{2}<lx,} a więc kwadrat rzędnej punktu elipsy jest mniejszy niż pole prostokąta o bokach długości równych parametrowi l{displaystyle l}l oraz odciętej. Ślad tej relacji można też zaobserwować w równaniu ogólnym stożkowej, ax2+2hxy+bx2+2gx+2fy+c=0,{displaystyle ax^{2}+2hxy+bx^{2}+2gx+2fy+c=0,}{displaystyle ax^{2}+2hxy+bx^{2}+2gx+2fy+c=0,} w którym elipsa charakteryzuje się spełnianiem nierówności h2<ab.{displaystyle h^{2}<ab.}{displaystyle h^{2}<ab.}



Kreślenie |




Elipsa narysowana za pomocą dwóch szpilek, pętli oraz długopisu.




Model elipsografu.



Metoda szpilek i sznurka |


Elipsę można nakreślić za pomocą dwóch szpilek (pinezek), kawałka sznurka i rysika (ołówka, długopisu):


Należy wetknąć szpilki w dwa punkty papieru, które staną się ogniskami elipsy, następnie zawiązać sznurek w luźną pętlę wokół szpilek, po czym naciągnąć sznurek za pomocą rysika tak, by powstał trójkąt. Elipsa zostanie nakreślona poprzez przesuwanie rysika po powierzchni kartki przy zachowaniu napięcia sznurka.

Aby nakreślić elipsę wpisaną w dany prostokąt, styczną do jego czterech boków w ich środkach, należy najpierw określić położenie ognisk i długość pętli:



Niech A,B,C,D{displaystyle A,B,C,D}{displaystyle A,B,C,D} będą wierzchołkami prostokąta danymi w porządku odwrotnym do wskazówek zegara, gdzie AB{displaystyle AB}AB jest jednym z dłuższych boków. Należy nakreślić okrąg o środku w A{displaystyle A}A i promieniu równym długości krótszego boku AD,{displaystyle AD,}{displaystyle AD,} a następnie wyznaczyć styczną do okręgu przechodzącą przez B.{displaystyle B.}B. Długość L{displaystyle L}L odcinka od B{displaystyle B}B do punktu styczności jest odległością między ogniskami. Należy następnie nakreślić dwie proste prostopadłe przez środek prostokąta równoległe do jego boków; będą to osie wielka i mała elipsy. Ogniska rozmieszczone są symetrycznie na osi wielkiej w odległości L2{displaystyle {tfrac {L}{2}}}{displaystyle {tfrac {L}{2}}} od środka.

Aby dostosować długość pętli sznurka należy wetknąć szpilkę w jedno z ognisk, drugą zaś w przeciwny (położony dalej) koniec osi głównej, po czym wykonać ścisłą pętlę wokół dwóch szpilek (tak, by była napięta). Oznacza to, że długość sznurka jest określona wzorem kk=2c+2a,{displaystyle k_{k}=2c+2a,}{displaystyle k_{k}=2c+2a,} gdzie 2c{displaystyle 2c}{displaystyle 2c} jest długością ogniskowej[a] a 2a{displaystyle 2a}2a to długość osi wielkiej.



Inne metody |


Elipsa może być także nakreślona za pomocą linijki, ekierki oraz rysika:


Należy nakreślić dwie proste prostopadłe M,N{displaystyle M,N}{displaystyle M,N} na papierze; będą to osie wielka i mała elipsy. Następnie na linijce należy oznaczyć punkty A,B,C.{displaystyle A,B,C.}A,B,C. Obracając jedną ręką linijkę tak, by punkt A{displaystyle A}A zawsze leżał na prostej M,{displaystyle M,}M, a punkt B{displaystyle B}B na prostej N{displaystyle N}N i kreśląc rysikiem za pomocą drugiej ręki na papierze, śladem punktu C{displaystyle C}C na linijce otrzymuje się elipsę.

Metoda ta może być wykorzystana przy cięciu elips z materiałów drewnianych za pomocą frezarek (ręcznych). Innym przyrządem korzystającym z tej zasady jest elipsograf lub cyrkiel drążkowy: linijka zastąpiona jest prętem z uchwytem na rysik (punkt C{displaystyle C}C) z jednej strony oraz dwoma przesuwnymi bolcami, które przesuwają się w dwóch prostopadłych prowadnicach wyciętych płycie.



Geometria analityczna |


Elipsa w pozycji kanonicznej opisana jest w układzie współrzędnych kartezjańskich (x,y){displaystyle (x,y)}{displaystyle (x,y)} równaniem


x2a2+y2b2=1,{displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1,}{displaystyle {frac {x^{2}}{a^{2}}}+{frac {y^{2}}{b^{2}}}=1,}

gdzie a{displaystyle a}a i b{displaystyle b}b są długościami półosi.


Elipsa w postaci parametrycznej dana jest jako


{x=acos⁡t,y=bsin⁡t,{displaystyle {begin{cases}x=acos t,\y=bsin t,end{cases}}}{displaystyle {begin{cases}x=acos t,\y=bsin t,end{cases}}}

gdzie:


0⩽t<2π.{displaystyle 0leqslant t<2pi .}{displaystyle 0leqslant t<2pi .}

W układzie współrzędnych biegunowych (r,θ){displaystyle (r,theta )}{displaystyle (r,theta )} elipsę opisuje wzór


r2=b21−e2cos2⁡θ=a2b2a2sin2θ+b2cos2θ,{displaystyle r^{2}={frac {b^{2}}{1-e^{2}cos ^{2}theta }}={frac {a^{2}b^{2}}{a^{2}sin^{2}theta +b^{2}cos^{2}theta }},}{displaystyle r^{2}={frac {b^{2}}{1-e^{2}cos ^{2}theta }}={frac {a^{2}b^{2}}{a^{2}sin^{2}theta +b^{2}cos^{2}theta }},}

gdzie e{displaystyle e}e jest mimośrodem.



Własności |



Pole i obwód |


Pole powierzchni ograniczonej przez elipsę opisuje wzór


S=πab.{displaystyle S=pi ab.}{displaystyle S=pi ab.}

Obwód elipsy jest dany tzw. całką eliptyczną i nie daje się w ogólnym przypadku zapisać w postaci algebraicznej. Przybliżony wzór na obwód elipsy


ℓ≈π(32(a+b)−ab),{displaystyle ell approx pi left({tfrac {3}{2}}(a+b)-{sqrt {ab}}right),}{displaystyle ell approx pi left({tfrac {3}{2}}(a+b)-{sqrt {ab}}right),}

lepszy


ℓ≈π[3(a+b)−(3a+b)(a+3b)]=π[3(a+b)−10ab+3(a2+b2)],{displaystyle ell approx pi left[3(a+b)-{sqrt {(3a+b)(a+3b)}};right]=pi left[3(a+b)-{sqrt {10ab+3(a^{2}+b^{2})}};right],}{displaystyle ell approx pi left[3(a+b)-{sqrt {(3a+b)(a+3b)}};right]=pi left[3(a+b)-{sqrt {10ab+3(a^{2}+b^{2})}};right],}

jeszcze lepszy



ℓ≈π(a+b)(1+3h10+4−3h){displaystyle ell approx pi left(a+bright)left(1+{frac {3h}{10+{sqrt {4-3h}}}}right)}{displaystyle ell approx pi left(a+bright)left(1+{frac {3h}{10+{sqrt {4-3h}}}}right)} gdzie h=(a−b)2/(a+b)2.{displaystyle h=(a-b)^{2}/(a+b)^{2}.}{displaystyle h=(a-b)^{2}/(a+b)^{2}.}

Dokładny wzór na obwód elipsy wyraża się następująco (E{displaystyle E}E to zupełna całka eliptyczna drugiego rodzaju, a e{displaystyle e}e to mimośród elipsy):


ℓ=4aE(e2)=4aE(1−b2a2)=4a∫0π21−e2sin2⁡θ dθ=4a∫011−e2t21−t2 dt.{displaystyle ell =4aE(e^{2})=4aEleft(1-{frac {b^{2}}{a^{2}}}right)=4aint _{0}^{frac {pi }{2}}{sqrt {1-e^{2}sin ^{2}theta }} dtheta =4aint _{0}^{1}{frac {sqrt {1-e^{2}t^{2}}}{sqrt {1-t^{2}}}} dt.}{displaystyle ell =4aE(e^{2})=4aEleft(1-{frac {b^{2}}{a^{2}}}right)=4aint _{0}^{frac {pi }{2}}{sqrt {1-e^{2}sin ^{2}theta }} dtheta =4aint _{0}^{1}{frac {sqrt {1-e^{2}t^{2}}}{sqrt {1-t^{2}}}} dt.}

Istnieją różne konwencje zapisu funkcji specjalnej E.{displaystyle E.}E. W niektórych argumentem jest nie kwadrat mimośrodu, ale sam mimośród; właściwy wzór pod samym znakiem całki będzie zawierał e{displaystyle e}e w drugiej potędze (nigdy w pierwszej czy czwartej).

Chcąc uzyskać długość łuku elipsy należy skorzystać z niezupełnej całki eliptycznej drugiego rodzaju[4].




Rys. 1 – własność stycznej



Styczna |


Styczna w punkcie P do elipsy o ogniskach F1, F2{displaystyle F_{1}, F_{2}}{displaystyle F_{1}, F_{2}} jest dwusieczną kąta zewnętrznego trójkąta ΔF1PF2.{displaystyle Delta F_{1}PF_{2}.}{displaystyle Delta F_{1}PF_{2}.} Jest to równoznaczne z tym, że promień świetlny wychodzący z jednego ogniska elipsy po odbiciu (zgodnie z zasadą, że kąt padania jest równy kątowi odbicia) od krawędzi elipsy przejdzie przez drugie ognisko (kolorowe kąty na rysunku 1 mają równe miary).




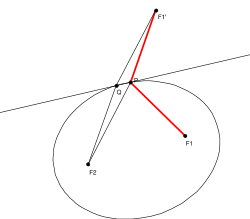
Dowód własności stycznej


Dowód

Załóżmy, że dwusieczna tego kąta nie jest styczną, czyli przecina elipsę w pewnym punkcie Q{displaystyle Q}Q różnym od P.{displaystyle P.}{displaystyle P.}


Niech F1′{displaystyle F_{1}'}{displaystyle F_{1}'} będzie odbiciem F1{displaystyle F_{1}}F_1 w dwusiecznej. Z symetrii wynika, że



F1P=F1′P,{displaystyle F_{1}P=F_{1}'P,}{displaystyle F_{1}P=F_{1}'P,} więc F2P+PF1′=2a,{displaystyle F_{2}P+PF_{1}'=2a,}{displaystyle F_{2}P+PF_{1}'=2a,}

gdzie a{displaystyle a}a oznacza długość dużej półosi elipsy. Podobnie pokazujemy, że


F2Q+QF1′=2a{displaystyle F_{2}Q+QF_{1}'=2a}{displaystyle F_{2}Q+QF_{1}'=2a}

Ponieważ kąt F1PF1′{displaystyle F_{1}PF_{1}'}{displaystyle F_{1}PF_{1}'} jest kątem zewnętrznym trójkąta F1PF2,{displaystyle F_{1}PF_{2},}{displaystyle F_{1}PF_{2},} to punkty F1′,P,F2{displaystyle F_{1}',P,F_{2}}{displaystyle F_{1}',P,F_{2}} są współliniowe, więc F1′,Q,F2{displaystyle F_{1}',Q,F_{2}}{displaystyle F_{1}',Q,F_{2}} są niewspółliniowe.


Stąd F2P+PF1′<F2Q+QF1′.{displaystyle F_{2}P+PF_{1}'<F_{2}Q+QF_{1}'.}{displaystyle F_{2}P+PF_{1}'<F_{2}Q+QF_{1}'.} Jest to sprzeczne z F2P+PF1′=2a=F2Q+QF1′.{displaystyle F_{2}P+PF_{1}'=2a=F_{2}Q+QF_{1}'.}{displaystyle F_{2}P+PF_{1}'=2a=F_{2}Q+QF_{1}'.}


Zakładając nieprawdziwość tezy, doszliśmy do sprzeczności, zatem teza została udowodniona.




Rys. 2 – własność dwóch stycznych



Dwie styczne |


Gdy z punktu S{displaystyle S}S leżącego na zewnątrz elipsy poprowadzimy dwie proste, styczne do elipsy w punktach K{displaystyle K}K i L,{displaystyle L,}L, to



∠KSF1=∠LSF2,{displaystyle angle KSF_{1}=angle LSF_{2},}{displaystyle angle KSF_{1}=angle LSF_{2},}

∠KF1S=∠LF1S.{displaystyle angle KF_{1}S=angle LF_{1}S.}{displaystyle angle KF_{1}S=angle LF_{1}S.}


(kąty o tych samych kolorach na rysunku 2 mają równe miary).


Dowód pierwszej równości



Dowód własności dwóch stycznych


Odbijamy elipsę w obu stycznych. Ogniska obrazów oznaczamy odpowiednio przez F1′, F1″, F2′, F2″.{displaystyle F_{1}', F_{1}'', F_{2}', F_{2}''.}{displaystyle F_{1}', F_{1}'', F_{2}', F_{2}''.}


Pamiętając własność stycznej udowodnioną powyżej, łatwo otrzymujemy, że F2F1′=F2F1″=2a{displaystyle F_{2}F_{1}'=F_{2}F_{1}''=2a}{displaystyle F_{2}F_{1}'=F_{2}F_{1}''=2a} (a{displaystyle a}a – duża półoś). Oprócz tego, SF1′=SF1″,{displaystyle SF_{1}'=SF_{1}'',}{displaystyle SF_{1}'=SF_{1}'',} bo są obrazami tego samego odcinka.


Zatem ΔSF2F1′=ΔSF2F1″,{displaystyle Delta SF_{2}F_{1}'=Delta SF_{2}F_{1}'',}{displaystyle Delta SF_{2}F_{1}'=Delta SF_{2}F_{1}'',}


więc ∠SF2F1′=∠SF2F1″{displaystyle angle SF_{2}F_{1}'=angle SF_{2}F_{1}''}{displaystyle angle SF_{2}F_{1}'=angle SF_{2}F_{1}''}


oraz ∠F2SF1′=∠F2SF1″.{displaystyle angle F_{2}SF_{1}'=angle F_{2}SF_{1}''.}{displaystyle angle F_{2}SF_{1}'=angle F_{2}SF_{1}''.}



∠F2SF1″=∠KSL+∠F1″SL−∠KSF2,{displaystyle angle F_{2}SF_{1}''=angle KSL+angle F_{1}''SL-angle KSF_{2},}{displaystyle angle F_{2}SF_{1}''=angle KSL+angle F_{1}''SL-angle KSF_{2},}


∠F2SF1′=∠KSL′+∠F2SK−∠L′SF1′,{displaystyle angle F_{2}SF_{1}'=angle KSL'+angle F_{2}SK-angle L'SF_{1}',}{displaystyle angle F_{2}SF_{1}'=angle KSL'+angle F_{2}SK-angle L'SF_{1}',} gdzie L′{displaystyle L'}L' – odbicie L{displaystyle L}L w SK.{displaystyle SK.}{displaystyle SK.}


Lewe części tych równości są równe, oraz, ∠KSL=∠KSL′;{displaystyle angle KSL=angle KSL';}{displaystyle angle KSL=angle KSL';} stąd ∠F2SK−∠L′SF1′=∠F1″SL−∠KSF2,{displaystyle angle F_{2}SK-angle L'SF_{1}'=angle F_{1}''SL-angle KSF_{2},}{displaystyle angle F_{2}SK-angle L'SF_{1}'=angle F_{1}''SL-angle KSF_{2},}


czyli 2∠KSF2=∠F1″SL+∠L′SF1′.{displaystyle 2angle KSF_{2}=angle F_{1}''SL+angle L'SF_{1}'.}{displaystyle 2angle KSF_{2}=angle F_{1}''SL+angle L'SF_{1}'.}


Ponieważ ∠L′SF1′=∠F1″SL,{displaystyle angle L'SF_{1}'=angle F_{1}''SL,}{displaystyle angle L'SF_{1}'=angle F_{1}''SL,}


to ∠KSF2=∠F1″SL=∠L′SF1′=∠LSF1.{displaystyle angle KSF_{2}=angle F_{1}''SL=angle L'SF_{1}'=angle LSF_{1}.}{displaystyle angle KSF_{2}=angle F_{1}''SL=angle L'SF_{1}'=angle LSF_{1}.}


Więc mamy ∠KSF2=∠LSF1,{displaystyle angle KSF_{2}=angle LSF_{1},}{displaystyle angle KSF_{2}=angle LSF_{1},} a stąd wynika równość ∠KSF1=∠LSF2,{displaystyle angle KSF_{1}=angle LSF_{2},}{displaystyle angle KSF_{1}=angle LSF_{2},} którą trzeba było udowodnić.




Rys. 3 – trójkąt opisany



Trójkąt opisany |


Gdy punkty F1, F2{displaystyle F_{1}, F_{2}}{displaystyle F_{1}, F_{2}} leżące wewnątrz trójkąta ABC spełniają



∠CBF1=∠ABF2,{displaystyle angle CBF_{1}=angle ABF_{2},}{displaystyle angle CBF_{1}=angle ABF_{2},}

∠BAF1=∠CAF2,{displaystyle angle BAF_{1}=angle CAF_{2},}{displaystyle angle BAF_{1}=angle CAF_{2},}


to istnieje elipsa o ogniskach F1, F2{displaystyle F_{1}, F_{2}}{displaystyle F_{1}, F_{2}} wpisana w trójkąt, czyli styczna do jego trzech boków (rys. 3). Wtedy zachodzi również ∠BCF1=∠ACF2.{displaystyle angle BCF_{1}=angle ACF_{2}.}{displaystyle angle BCF_{1}=angle ACF_{2}.} Szczególnym przypadkiem takiej elipsy jest elipsa o ogniskach w ortocentrum i środku okręgu opisanego na trójkącie.


Dowód

Możemy tak dobrać dużą półoś elipsy, żeby była styczna do AB.{displaystyle AB.}{displaystyle AB.} Z twierdzenia odwrotnego do powyższej własności o dwóch stycznych (które jest oczywistą konsekwencją tej własności) mamy, że jest ona styczna do pozostałych boków trójkąta, bo zachodzą równości odpowiednich kątów. Korzystając ponownie z własności stycznych, otrzymujemy równość ∠BCF1=∠ACF2.{displaystyle angle BCF_{1}=angle ACF_{2}.}{displaystyle angle BCF_{1}=angle ACF_{2}.}


Dokonując rachunku na kątach, otrzymujemy powyższe równości dla ortocentrum i środka okręgu opisanego, z czego wynika, że istnieje elipsa wpisana w trójkąt o takich ogniskach.




Rys. 4 – okrąg opisany



Okrąg opisany |


Niech X{displaystyle X}X będzie rzutem prostokątnym ogniska elipsy na styczną do niej. Miejscem geometrycznym wszystkich punktów X{displaystyle X}X jest okrąg o środku w środku odcinka łączącego ogniska i o promieniu równym dużej półosi elipsy (czerwony okrąg na rys. 4).


Dowód



Dowód twierdzenia o okręgu opisanym


Poprowadźmy dwie równoległe styczne do elipsy w punktach X, Y.{displaystyle X, Y.}{displaystyle X, Y.} Są one symetryczne względem środka S{displaystyle S}S elipsy, więc F1XF2Y{displaystyle F_{1}XF_{2}Y}{displaystyle F_{1}XF_{2}Y} jest równoległobokiem.


Niech A, D{displaystyle A, D}{displaystyle A, D} będą rzutami prostokątnymi ognisk F1, F2{displaystyle F_{1}, F_{2}}{displaystyle F_{1}, F_{2}} na styczną w Y,{displaystyle Y,}Y, zaś B, C{displaystyle B, C}{displaystyle B, C} na styczną w X.{displaystyle X.}X. Odbijamy X{displaystyle X}X w prostej AB,{displaystyle AB,}{displaystyle AB,} otrzymując punkt X′.{displaystyle X'.}{displaystyle X'.}


Punkty B, D{displaystyle B, D}{displaystyle B, D} są symetryczne względem S,{displaystyle S,}S, więc BX′=BX=YD.{displaystyle BX'=BX=YD.}{displaystyle BX'=BX=YD.}


Stąd BDYX′{displaystyle BDYX'}{displaystyle BDYX'} jest równoległobokiem, czyli BD=YX′.{displaystyle BD=YX'.}{displaystyle BD=YX'.}


Ale YX′=YF1+F1X′=YF1+F1X.{displaystyle YX'=YF_{1}+F_{1}X'=YF_{1}+F_{1}X.}{displaystyle YX'=YF_{1}+F_{1}X'=YF_{1}+F_{1}X.}


Więc BD=YF1+YF2=2a,{displaystyle BD=YF_{1}+YF_{2}=2a,}{displaystyle BD=YF_{1}+YF_{2}=2a,} gdzie a{displaystyle a}a – duża półoś (korzystamy z równości wynikających z istnienia odpowiednich równoległoboków).


BD{displaystyle BD}{displaystyle BD} jest średnicą okręgu opisanego na prostokącie ABCD, którego środkiem jest S{displaystyle S}S więc BS=DS=a,{displaystyle BS=DS=a,}{displaystyle BS=DS=a,} co należało pokazać.



Uogólnienia |


Elipsa jest szczególnym przypadkiem superelipsy. Odpowiednikiem elipsy w przestrzeni trójwymiarowej jest elipsoida.



Zobacz też |















Informacje w projektach siostrzanych

Commons-logo.svg  Multimedia w Wikimedia Commons

Wikiquote-logo.svg  Cytaty w Wikicytatach

WiktionaryPl nodesc.svg  Definicje słownikowe w Wikisłowniku

  • całka eliptyczna


Uwagi |




  1. ↑ Tak nazywa się czasem odległość między ogniskami.



Przypisy |




  1. ↑ Władysław Kopaliński: elipsa; elipsoida; eliptyczny. W: Słownik wyrazów obcych i zwrotów obcojęzycznych [on-line]. [dostęp 2018-07-16].


  2. ↑ Henry George Liddell, Robert Scott: ἔλλειψις (ang.). W: A Greek-English Lexicon [on-line]. [dostęp 2018-07-16].


  3. ↑ dr inż. Paweł Pędzich: Kartografia matematyczna. Zakład Kartografii Politechniki Warszawskiej. [dostęp 2014-03-06].


  4. ↑ Dokładniejsze informacje można znaleźć na stronie Wolfram MathWorld o elipsie.



Linki zewnętrzne |



  • Elipsa (ang.) w encyklopedii MathWorld



-

這個網誌中的熱門文章

12.7 cm/40 Type 89 naval gun

圖片
12.7 cm/40 Type 89 naval gun Type 89 gun mounted on Chitose Type Naval gun anti-aircraft gun Place of origin Japan Service history In service 1932–45 Used by Imperial Japanese Navy Wars World War II Production history Designed 1928–32 Produced 1932–45 No.  built ~1500 Variants Type 88 Specifications Mass 3,100 kilograms (6,834 lb) Barrel length 5,080 millimeters (16 ft 8 in) (bore length) Shell Fixed Shell weight 20.9–23.45 kilograms (46.1–51.7 lb) Caliber 12.7-centimeter (5.0 in) Breech horizontal breech block Elevation -8° to +90° [1] Rate of fire 8-14 rounds per minute Muzzle velocity 720–725 meters per second (2,360–2,380 ft/s) Maximum firing range 9,440 meters (30,970 ft) at 90° (AA ceiling) 14,800 meters (48,600 ft) at 45° The 12.7 cm/40 Type 89 naval gun was a Japanese anti-aircraft (AA) gun introduced before World War II. It was the Imperial Japanese Navy's standard heavy AA
閱讀完整內容

Shark

圖片
For other uses, see Shark (disambiguation). Sharks Temporal range: Ludfordian-Present, 425–0 Ma PreЄ Є O S D C P T J K Pg N [1] Clockwise from top left: spiny dogfish, Japanese sawshark, whale shark, great white shark, horn shark, frilled shark, scalloped hammerhead and Australian angelshark representing the orders Squaliformes, Pristiophoriformes, Orectolobiformes, Lamniformes, Heterodontiformes, Hexanchiformes, Carcharhiniformes and Squatiniformes respectively. Scientific classification Kingdom: Animalia Phylum: Chordata Class: Chondrichthyes Subclass: Elasmobranchii Infraclass: Euselachii Superorder: Selachimorpha Orders Carcharhiniformes Heterodontiformes Hexanchiformes Lamniformes Orectolobiformes Pristiophoriformes Squaliformes Squatiniformes † Cladoselachiformes † Hybodontiformes † Symmoriida † Xenacanthida (Xenacantiformes) † Elegestolepis † = extinct Synonyms Pleurotremata Sharks
閱讀完整內容

Wiciokrzew

圖片
Wiciokrzew, suchodrzew Morfologia (wiciokrzew pospolity) Systematyka [1] Domena eukarionty Królestwo rośliny Klad rośliny naczyniowe Klad rośliny nasienne Klasa okrytonasienne Klad astrowe Rząd szczeciowce Rodzina przewiertniowate Rodzaj wiciokrzew Nazwa systematyczna Lonicera L. Sp. Pl. 173. 1 Mai 1753 Typ nomenklatoryczny Lonicera caprifolium L. [2] Multimedia w Wikimedia Commons Hasło w Wikisłowniku Kwiaty suchodrzewu pospolitego Owoce suchodrzewu pospolitego Kwiaty wiciokrzewu pomorskiego Kwiaty wiciokrzewu przewiercienia Wiciokrzew , suchodrzew ( Lonicera L.) – rodzaj roślin wieloletnich należący do rodziny przewiertniowatych ( Caprifoliaceae ). Rośliny zielne i pnące nazywane są wiciokrzewami, natomiast krzewy i niewielkie drzewa – suchodrzewami. Rodzaj liczy około 180 gatunków szeroko rozprzestrzenionych na całej półkuli północnej [3] [4]
閱讀完整內容