Egftnjytyk

Ten artykuł dotyczy pojęcia pierwotnego matematyki. Zobacz też: inne znaczenia tego słowa.

Zbiór (dawniej także mnogość^[1]) – pojęcie pierwotne aksjomatycznej teorii mnogości leżące u podstaw całej matematyki^[1]; idealizacja intuicyjnie rozumianego zbioru (zestawu, kolekcji) utworzonego z elementów (komponentów, składowych), która jest efektem abstrahowania od wewnętrznej struktury modelowanego obiektu i wzajemnych zależności między jego elementami (np. hierarchii, czy kolejności).

Wprowadzenie |

Każdy zbiór jest jednoznacznie wyznaczony przez swoją zawartość (tzn. istnieje tylko jeden zbiór złożony z zadanych elementów), przy czym każdy element może należeć do danego zbioru bądź nie (tzn. element nie może należeć do zbioru np. „dwukrotnie”). Pojęcie zbioru ma charakter dystrybutywny, a nie kolektywny: Mars jest elementem zbioru planet Układu Słonecznego, lecz jakikolwiek element tej planety, np. leżąca na niej skała, nie jest już elementem wspomnianego zbioru planet (dystrybutywność); nadwozie jest elementem zbioru części samochodu, przy czym wycieraczka jest elementem nadwozia, a więc jest elementem samochodu (kolektywność).

W tzw. naiwnej (tj. niezaksjomatyzowanej) teorii mnogości zbiory wprowadza się wraz z relacją ∈{displaystyle in } należenia lub przynależności do zbioru^[a] oznaczaną zmodyfikowaną małą literą alfabetu greckiego ϵ{displaystyle epsilon } (dla odróżnienia w matematyce korzysta się z innego jej wariantu typograficznego, ε{displaystyle varepsilon }); przykładowo należenie elementu a{displaystyle a} do zbioru A{displaystyle A} zapisuje się zwykle a∈A,{displaystyle ain A,} zaś zaprzeczenie tego zdania („element a{displaystyle a} nie należy do zbioru A{displaystyle A}”) uzyskuje się poprzez przekreślenie znaku relacji należenia: a∉A{displaystyle anotin A}^[b].

Elementy danego zbioru zwykło się zapisywać w nawiasach klamrowych; przykładowo zbiór składający się z czterech elementów ★,3,♠,¶{displaystyle bigstar ,3,spadesuit ,P } zapisuje się zwykle symbolicznie w postaci

{★,3,♠,¶};{displaystyle {bigstar ,3,spadesuit ,P };}

jest to jedyny zbiór składający się z tych elementów, co oznacza, że napisy {3,★,♠,¶},{displaystyle {3,bigstar ,spadesuit ,P },} czy {¶,★,3,♠}{displaystyle {P ,bigstar ,3,spadesuit }} (kolejność podawania elementów nie ma znaczenia), bądź {★,¶,3,★,♠,♠}{displaystyle {bigstar ,P ,3,bigstar ,spadesuit ,spadesuit }} (wielokrotne wymienienie tego samego elementu niczego nie przydaje) oznaczają ten sam zbiór. Poniekąd najprostszym, choć dość nieintuicyjnym zbiorem jest zbiór nie zawierający żadnego elementu, tzw. zbiór pusty {}{displaystyle {}} oznaczany zwykle symbolem ∅.{displaystyle varnothing .} Elementami zbiorów mogą być również inne zbiory – zbiory złożone ze zbiorów nazywa się zwykle rodzinami (zbiorów). Należy wyraźnie zaznaczyć, że zbiór ∅{displaystyle varnothing } nie ma elementów, podczas gdy do zbioru {∅}{displaystyle {varnothing }} należy jeden element: zbiór pusty ∅{displaystyle varnothing } (jest to więc jednoelementowa rodzina zbiorów złożona ze zbioru pustego).

Nie ma żadnego ograniczenia nałożonego na liczebność zbiorów, nazywaną ich mocą – moc zbioru A{displaystyle A} oznaczana będzie dalej symbolem #A{displaystyle #A} – wyróżnia się nawet różne hierarchie wielkości zbiorów związane z ich licznością (np. skala alefów, czy skala betów).

Określanie |

Wyszczególnienie wszystkich elementów danego zbioru może być co najmniej nużące (gdy zbiór jest skończony), a niekiedy nawet niemożliwe (gdy zbiór jest nieskończony). Jednym ze sposobów skrócenia tego zapisu jest wykorzystanie notacji wielokropkowej, która zakłada pewną domyślność czytelnika; przykładowo zbiór zawierający wszystkie nieparzyste liczby naturalne większe od 2,{displaystyle 2,} lecz mniejsze od 84,{displaystyle 84,} można wskazać zapisując

{3,5,7,…,81,83}.{displaystyle {3,5,7,dots ,81,83}.}

Należy jednak uważać, by zapis był dostatecznie jednoznaczny, np. {3,5,7,…,83}{displaystyle {3,5,7,dots ,83}} może oznaczać także zbiór liczb pierwszych ze wspomnianego przedziału, z kolei {3,…,83}{displaystyle {3,dots ,83}} może oznaczać wszystkie liczby naturalne z podanego zakresu.

Innym sposobem jest użycie formuły logicznej (warunku logicznego), jeśli W(x){displaystyle W(x)} jest zdaniem logicznym o elemencie x{displaystyle x} zbioru X,{displaystyle X,} to zapis

{x∈X:W(x)}{displaystyle {big {}xin Xcolon W(x){big }}}

oznacza zbiór wszystkich elementów x∈X,{displaystyle xin X,} które spełniają warunek W(x).{displaystyle W(x).}

W początkach teorii mnogości stosowano notację {x:W(x)},{displaystyle {xcolon W(x)},} tzn. nie ograniczano się do wybierania elementów z ustalonego zbioru – okazało się jednak, że prowadzi to do sprzeczności takich jak paradoks zbioru wszystkich zbiorów, czy antynomia Russella. Wspomniane problemy związane z konstruowaniem zbiorów były impulsem do formalizacji teorii mnogości poprzez porzucenie naiwnej teorii zbiorów na rzecz różnych aksjomatyzacji pojęć zbioru i relacji należenia; jedną z najczęściej stosowanych jest aksjomatyka Zermela-Fraenkla (w jednym ze swych wariantów)^[c].

Relacje |

 Osobne artykuły: podzbiór i aksjomat ekstensjonalności.

Przykładowe relacje pomiędzy zbiorami: rozłączność (A i D), posiadanie pewnych elementów wspólnych (A i C), zawieranie, czyli inkluzja (B w A).

W ogólności, dwa dowolne zbiory A{displaystyle A} i B{displaystyle B} mogą:

• być rozłączne, jeżeli nie posiadają wspólnych elementów;


• 
  przecinać się, czyli mieć niepustą część wspólną, jeżeli mają pewne elementy wspólne;


• być w relacji inkluzji, czyli zawierania. Zbiór B{displaystyle B} jest zawarty w A{displaystyle A} (jest podzbiorem zbioru A{displaystyle A}) wtedy i tylko wtedy, gdy każdy element zbioru B{displaystyle B} należy do zbioru A{displaystyle A}^[2][3]:

B⊆A⇔(x∈B⇒x∈A);{displaystyle Bsubseteq ALeftrightarrow (xin BRightarrow xin A);}

• być równe, jeżeli mają wszystkie elementy wspólne:

A=B⇔∀x∈Ω(x∈A⇔x∈B){displaystyle A=BLeftrightarrow forall _{xin Omega }(xin ALeftrightarrow xin B)}^[4]⇔(A⊆B∧B⊆A){displaystyle Leftrightarrow (Asubseteq Bland Bsubseteq A)}^[3].

Warunek równości zbiorów nazywany jest aksjomatem ekstensjonalności. Mówi on, że dwa zbiory są równe wtedy i tylko wtedy, gdy mają te same elementy. Zatem każdy zbiór jest jednoznacznie wyznaczony przez swoje elementy.

Równość zbiorów jest przykładem relacji równoważności, natomiast inkluzja jest relacją częściowego porządku. Innym przykładem relacji równoważności wśród zbiorów jest równoliczność.

Działania |

 Osobne artykuły: suma, iloczyn, różnica, dopełnienie i różnica symetryczna.

• 
  

  

  
  

  
  

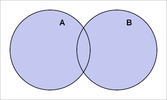
  Suma A∪B{displaystyle Acup B} oznaczona kolorem ciemnoniebieskim.
  

  
  

  
  


• 
  

  

  
  

  
  

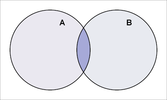
  Iloczyn A∩B{displaystyle Acap B} oznaczony kolorem ciemnoniebieskim.
  

  
  

  
  


• 
  

  

  
  

  
  

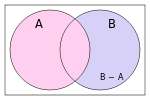
  Różnica B∖A{displaystyle Bsetminus A} oznaczona kolorem ciemnoniebieskim.
  

  
  

  
  


• 
  

  

  
  

  
  

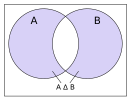
  Różnica symetryczna A△B{displaystyle Atriangle B} oznaczona kolorem ciemnoniebieskim.
  

  
  

  
  

Niech dane będą dowolne trzy podzbiory A,B{displaystyle A,B} oraz C{displaystyle C} zbioru Ω{displaystyle Omega } nazywanego przestrzenią lub uniwersum.

Definicje

• 
  Sumą A∪B{displaystyle Acup B} nazywa się zbiór tych elementów, które należą przynajmniej do jednego ze zbiorów A{displaystyle A} lub B{displaystyle B}^[5][6][7],
  

  A∪B={x∈Ω:x∈A∨x∈B}.{displaystyle Acup B={xin Omega colon xin Alor xin B}.}

  
  


• 
  Iloczynem A∩B{displaystyle Acap B} nazywa się zbiór tych elementów, które należą jednocześnie do obu zbiorów A{displaystyle A} oraz B{displaystyle B}^[6][8][9],
  

  A∩B={x∈Ω:x∈A∧x∈B}.{displaystyle Acap B={xin Omega colon xin Aland xin B}.}

  
  


• 
  Różnicą A∖B{displaystyle Asetminus B} nazywa się zbiór tych elementów, które należą do zbioru A,{displaystyle A,} ale nie należą do zbioru B{displaystyle B}^[6][7][10],
  

  A∖B={x∈Ω:x∈A∧x∉B}=A∩Bc.{displaystyle Asetminus B={xin Omega colon xin Aland xnotin B}=Acap B^{mathrm {c} }.}

  
  


• 
  Dopełnieniem Bc{displaystyle B^{mathrm {c} }} nazywa się zbiór tych elementów przestrzeni Ω,{displaystyle Omega ,} które nie należą do zbioru B{displaystyle B}^[11][12],
  

  Bc={x∈Ω:x∉B}=Ω∖B.{displaystyle B^{mathrm {c} }={xin Omega colon xnot in B}=Omega setminus B.}

  
  


• 
  Różnicą symetryczną A△B{displaystyle Atriangle B} nazywa się zbiór tych elementów, które należą do jednego i tylko jednego ze zbiorów A{displaystyle A} oraz B{displaystyle B}^[13][14],
  

  A△B={x∈Ω:x∈A ∨_ x∈B}=(A∖B)∪(B∖A).{displaystyle Atriangle B={xin Omega colon xin A {underline {lor }} xin B}=(Asetminus B)cup (Bsetminus A).}

  
  

Własności

• 
  łączność sumy i iloczynu (umożliwia wykonywanie jednakowych działań w dowolnej kolejności),
  

  
  

  
  (A∪B)∪C=A∪(B∪C){displaystyle (Acup B)cup C=Acup (Bcup C)}^[15][16][17],

  
  

  
  (A∩B)∩C=A∩(B∩C){displaystyle (Acap B)cap C=Acap (Bcap C)}^[8][16][17],

  
  

  
  


• 
  przemienność sumy i iloczynu (umożliwia zamianę wykonywania kolejności działania),
  

  
  

  
  A∪B=B∪A{displaystyle Acup B=Bcup A}^[15][16][17],

  
  

  
  A∩B=B∩A{displaystyle Acap B=Bcap A}^[8][16][17],

  
  

  
  


• 
  rozdzielność sumy względem iloczynu i iloczynu względem sumy,
  

  
  

  
  A∪(B∩C)=(A∪B)∩(A∪C){displaystyle Acup (Bcap C)=(Acup B)cap (Acup C)}^[16][18][19],

  
  

  
  A∩(B∪C)=(A∩B)∪(A∩C){displaystyle Acap (Bcup C)=(Acap B)cup (Acap C)}^[16][18][19],

  
  

  
  


• 
  I i II prawo De Morgana,
  

  
  

  
  (A∪B)c=Ac∩Bc{displaystyle (Acup B)^{mathrm {c} }=A^{mathrm {c} }cap B^{mathrm {c} }}^[12][20][21],

  
  

  
  (A∩B)c=Ac∪Bc{displaystyle (Acap B)^{mathrm {c} }=A^{mathrm {c} }cup B^{mathrm {c} }}^[12][20][21].

  
  

  
  

Przykłady

Niech A={1,2,3,5}{displaystyle A={1,2,3,5}} oraz B={1,3,4},{displaystyle B={1,3,4},} a ponadto Ω={1,2,3,…}.{displaystyle Omega ={1,2,3,dots }.} Wówczas

A∪B=B∪A={1,2,3,4,5},{displaystyle Acup B=Bcup A={1,2,3,4,5},}

A∩B=B∩A={1,3},{displaystyle Acap B=Bcap A={1,3},}

A∖B={2,5} oraz B∖A={4},{displaystyle Asetminus B={2,5}{text{ oraz }}Bsetminus A={4},}

Ac={4,6,7,8,…} oraz Bc={2,5,6,7,…},{displaystyle A^{mathrm {c} }={4,6,7,8,dots }{text{ oraz }}B^{mathrm {c} }={2,5,6,7,dots },}

A△B=B△A={2,4,5}.{displaystyle Atriangle B=Btriangle A={2,4,5}.}

Uwagi

Działania na zbiorach nazywa się często „mnogościowymi” dla odróżnienia od innych działań, np. algebraicznych: „suma mnogościowa”, „iloczyn mnogościowy”, „różnica mnogościowa” (lub nawet „suma, iloczyn, różnica zbiorów”). Działanie dodawania nazywa się niekiedy „unią”, z kolei różnicę nazywa się czasem „dopełnieniem względnym” (względem innego zbioru); dopełnienie bywa nazywane „uzupełnieniem”^[21]. Alternatywne nazwy „przekrój”, czy „przecięcie” dla iloczynu są spotykane dużo częściej.

Wraz z osobnymi nazwami działania te mają unikatową symbolikę, choć niekiedy różnicę zbiorów oznacza się znakiem odejmowania^[d], zaś dopełnienie oznacza się często apostrofem^[e], działanie różnicy symetrycznej wydaje się mieć najmniej ustaloną symbolikę: czasami stosuje się symbol dodawania w okręgu^[f]; odpowiednio A−B, A′, A⊕B.{displaystyle A-B, A', Aoplus B.}

Nazwy i symbole działań na zbiorach odwołujące się do intuicji algebraicznych nie są przypadkowe: niektóre z przedstawionych działań umożliwiają wprowadzenie na podzbiorach danego zbioru różnych struktur algebraicznych (np. ciało zbiorów, pierścień zbiorów itp.), w ogólności wszystkie tworzą one tzw. algebrę Boole’a.

W przypadku działań sumy i iloczynu rozpatruje się również operacje skończone (zdefiniowane indukcyjnie) i nieskończone (zdefiniowane za pomocą kwantyfikatorów, czyli logiki pierwszego rzędu; nazywane też uogólnionymi). Sumę rodziny zbiorów definiuje się jako zbiór tych elementów, dla których istnieje (choć jeden) sumowany zbiór, do którego należą, z kolei iloczyn rodziny zbiorów zawiera wyłącznie te elementy, które należą do wszystkich zbiorów będących czynnikami.

Uogólnienia |

 Osobne artykuły: para uporządkowana, iloczyn kartezjański i zbiór potęgowy.

Zbiór dwuelementowy złożony z dwóch (różnych) elementów a,b,{displaystyle a,b,} nazywany parą (nieuporządkowaną), nie zawiera w sobie informacji o kolejności swoich elementów, tj. {a,b}={b,a};{displaystyle {a,b}={b,a};} istnieje jednak obiekt nazywany parą uporządkowaną, który ją niesie, tj. (a,b)≠(b,a){displaystyle (a,b)neq (b,a)} – w teorii mnogości definiuje się go zwykle jako zbiór dwuelementowy:

(a,b)={{a},{a,b}}.{displaystyle (a,b)={{a},{a,b}}.}

Iloczynem kartezjańskim A×B{displaystyle Atimes B} zbiorów A,B{displaystyle A,B} nazywa się zbiór wszystkich par uporządkowanych, których pierwszy element należy do zbioru A,{displaystyle A,} a drugi do zbioru B;{displaystyle B;} ze względu na uporządkowanie par jest A×B≠B×A,{displaystyle Atimes Bneq Btimes A,} o ile czynniki są różne.

Zbiór potęgowy P(A){displaystyle {mathcal {P}}(A)} zbioru A{displaystyle A} to rodzina (zbiór zawierający) wszystkie podzbiory zbioru A;{displaystyle A;} zachodzi #P(A)=2#A.{displaystyle #{mathcal {P}}(A)=2^{#A}.}

Istnieje wiele uogólnień pojęcia zbioru, wśród nich są m.in.:

• 
  klasa – skupisko elementów dzielących wspólną właściwość;


• 
  multizbiór – zestaw bytów, w którym dany element może występować wielokrotnie;


• 
  n-tka – multizbiór, z określoną kolejnością elementów;


• 
  zbiór rozmyty – zbiór, do którego elementy należą w pewnym stopniu z przedziału [0, 1], gdzie 0 oznacza pełną nieprzynależność, a 1 pełną przynależność do zbioru, dopuszczalna jest tu zatem częściowa przynależność elementu do zbioru rozmytego;


• 
  zbiór przybliżony – zbiór odzwierciedlający logikę trójwartościową.

Zobacz też |

Zobacz hasło zbiór w Wikisłowniku

Zobacz podręcznik w Wikibooks: Matematyka dla liceum – Pojęcie zbioru

• rodzina indeksowana


• rodzina zbiorów


• suma rozłączna

Uwagi |

Przypisy |

Bibliografia |

• Zbiór. W: Grzegorz Andrzejczak [i in.]: Matematyka. Włodzimierz Waliszewski (red.). Warszawa: Wydawnictwa Szkolne i Pedagogiczne, 1988, s. 327, seria: Encyklopedia szkolna. ISBN 83-02-02551-8.


• Helena Rasiowa: Wstęp do matematyki współczesnej. Wyd. 5. Warszawa: PWN, 1975, seria: Biblioteka matematyczna, t. 30. OCLC 749626864.


• Kazimierz Kuratowski: Wstęp do teorii mnogości i topologii. Wyd. 8. Warszawa: PWN, 1980, seria: Biblioteka matematyczna, t. 9. ISBN 83-01-01372-9.


• Algebra zbiorów. W: Kazimierz Kuratowski, Andrzej Mostowski: Teoria mnogości. Warszawa: Polskie Towarzystwo Matematyczne, 1952, seria: Monografie matematyczne, t. 27. OCLC 250182901.