Egftnjytyk

Układ współrzędnych biegunowych (układ współrzędnych polarnych) – układ współrzędnych na płaszczyźnie wyznaczony przez pewien punkt O zwany biegunem oraz półprostą OS o początku w punkcie O zwaną osią biegunową.

Definicja |

Każdemu punktowi P płaszczyzny przypisujemy jego współrzędne biegunowe, jak następuje^[1]:

• 
  promień wodzący punktu P to jego odległość |OP| od bieguna,


• 
  amplituda punktu P to wartość kąta skierowanego pomiędzy półprostą OS a wektorem OP→.{displaystyle {overrightarrow {OP}}.}
  

Dla jednoznaczności przyjmuje się, że współrzędne bieguna O są równe (0,0).{displaystyle (0,0).} O amplitudzie możemy zakładać, że 0⩽φ<2π{displaystyle 0leqslant varphi <2pi } (niektórzy autorzy przyjmują −π<φ⩽π{displaystyle -pi <varphi leqslant pi }).

Rys historyczny |

Układ współrzędnych biegunowych został wprowadzony i rozwinięty w Europie w XVII wieku. Według Juliana Coolidge’a^[2] pierwszeństwo w używaniu tego układu należy przyznać albo Grégoire de Saint-Vincentowi lub Bonaventurze Cavalieriemu.

• Cavalieri^[3] użył współrzędnych biegunowych aby wyznaczyć pole obszaru ograniczonego spiralą Archimedesa (a ściślej mówiąc jej pierwszym „obrotem”).


• W 1647 de Saint-Vincent opublikował pracę, w której używał współrzędnych biegunowych i twierdził, że znał tę metodę już w 1625.


• W 1658, Blaise Pascal używa układu biegunowego w wyznaczeniu długości pewnych łuków. Trzy lata później podobnej metody użył szkocki matematyk James Gregory.


• 
  Isaac Newton^[4] dyskutuje różne układy współrzędnych i w pewnych przypadkach używa układu biegunowego.


• Za twórcę biegunowego układu współrzędnych w jego współczesnej formie uważa się Jakoba Bernoulliego, który używał tego układu w badaniach krzywizny pewnych krzywych.

Związek z układem kartezjańskim |

Rysunek pokazujący związek układów biegunowego i kartezjańskiego

Rozważmy dwa układy współrzędnych na płaszczyźnie: układ kartezjański OXY{displaystyle OXY} oraz układ biegunowy z biegunem O{displaystyle O} i osią biegunową OX.{displaystyle OX.}

Przejście od układu biegunowego do kartezjańskiego |

Dla danego wektora wodzącego r⩾0{displaystyle rgeqslant 0} i amplitudy φ∈[0,2π){displaystyle varphi in [0,2pi )} punktu P, jego współrzędne kartezjańskie są określone wzorami^[5][6]:

x=r⋅cos⁡φ,{displaystyle x=rcdot cos varphi ,}

y=r⋅sin⁡φ.{displaystyle y=rcdot sin varphi .}

Jakobian przejścia wynosi

D(x,y)D(r,φ)=|∂x∂r∂x∂φ∂y∂r∂y∂φ|=|cos⁡φ−rsin⁡φsin⁡φrcos⁡φ|{displaystyle {frac {D(x,y)}{D(r,varphi )}}=left|{begin{matrix}{frac {partial x}{partial r}}&{frac {partial x}{partial varphi }}\{frac {partial y}{partial r}}&{frac {partial y}{partial varphi }}end{matrix}}right|=left|{begin{matrix}cos varphi &-rsin varphi \sin varphi &rcos varphi end{matrix}}right|} =r(cos2⁡φ+sin2⁡φ)=r.{displaystyle =r(cos ^{2}varphi +sin ^{2}varphi )=r.}

Przejście od układu kartezjańskiego do biegunowego |

Rozważmy punkt o współrzędnych kartezjańskich (x,y).{displaystyle (x,y).} Promień wodzący tego punktu może być wyznaczony na podstawie twierdzenia Pitagorasa:

r=x2+y2{displaystyle r={sqrt {x^{2}+y^{2}}}}^[7][6].

Jeśli r≠0{displaystyle rneq 0} i x≠0,{displaystyle xneq 0,} to z definicji funkcji tangens:

tgφ=yx{displaystyle operatorname {tg} ,varphi ={tfrac {y}{x}}}^[7],

zatem amplituda φ{displaystyle varphi } tego punktu jest dana wzorem:

φ=arctg(yx){displaystyle varphi =operatorname {arctg} ;({tfrac {y}{x}})}^[8]

(o ile dopuszczamy ujemne wartości φ{displaystyle varphi }).

Natomiast aby otrzymać 0⩽φ<2π,{displaystyle 0leqslant varphi <2pi ,} należy rozważyć następujące przypadki:

φ={arctg(yx),gdy x>0 oraz y⩾0arctg(yx)+2π,gdy x>0 oraz y<0arctg(yx)+π,gdy x<0π2,gdy x=0 oraz y>03π2,gdy x=0 oraz y<0,{displaystyle varphi ={begin{cases}operatorname {arctg} ;({tfrac {y}{x}}),&{mbox{gdy }}x>0{mbox{ oraz }}ygeqslant 0\operatorname {arctg} ;({tfrac {y}{x}})+2pi ,&{mbox{gdy }}x>0{mbox{ oraz }}y<0\operatorname {arctg} ;({tfrac {y}{x}})+pi ,&{mbox{gdy }}x<0\{tfrac {pi }{2}},&{mbox{gdy }}x=0{mbox{ oraz }}y>0\{tfrac {3pi }{2}},&{mbox{gdy }}x=0{mbox{ oraz }}y<0end{cases}},}

gdzie arctg{displaystyle operatorname {arctg} } oznacza funkcję arcus tangens. W zakresie kątów (−π,π){displaystyle (-pi ,pi )} można ten zapis uprościć do

φ=arccos⁡(xr)sgn⁡(y),{displaystyle varphi =arccos({tfrac {x}{r}});operatorname {sgn} (y),}

gdzie sgn{displaystyle operatorname {sgn} } oznacza funkcję signum.

Krzywe w układzie biegunowym |

Dla szeregu krzywych algebraicznych ich równania przedstawione w układzie biegunowym cechują się dużą symetrią lub pewną prostotą. Równania te nazywamy równaniami biegunowymi krzywych.

Okrąg |

Okrąg o równaniu r=1{displaystyle r=1}

Okrąg o środku w punkcie (r0,φ0){displaystyle (r_{0},varphi _{0})} i promieniu a>0{displaystyle a>0} jest opisany przez równanie

r2−2rr0cos⁡(φ−φ0)+r02=a2.{displaystyle r^{2}-2rr_{0}cos(varphi -varphi _{0})+r_{0}^{2}=a^{2}.}

W szczególnym przypadku gdy środek znajduje się w biegunie układu współrzędnych, powyższe równanie przybiera szczególnie prostą postać:

r=a.{displaystyle r=a.}

Róża |

Róża o równaniu r=2sin⁡(4φ){displaystyle r=2sin(4varphi )}

Krzywa znana pod nazwą róży lub róży polarnej opisana jest przez równanie

r=acos⁡(kφ+φ0),{displaystyle r=acos(kvarphi +varphi _{0}),}

gdzie φ0{displaystyle varphi _{0}} jest dowolną stałą, a{displaystyle a} jest parametrem wyznaczającym długość „płatków” róży, a k jest parametrem wyznaczającym ilość i formę „płatków” róży.
Jeśli k jest nieparzystą liczbą całkowitą, to róża będzie miała k płatków, a jeśli k jest parzystą liczbą całkowitą, to róża będzie miała 2k{displaystyle 2k} płatków. Dla innych wartości k kształt krzywej może być bardziej skomplikowany.

Spirala Archimedesa |

Jedno ramię spirali Archimedesa o równaniu r=φ{displaystyle r=varphi } dla 0<φ<6π{displaystyle 0<varphi <6pi }

Spirala Archimedesa jest przedstawiona przez równanie

r=a+bφ.{displaystyle r=a+bvarphi .}

Parametry a,b{displaystyle a,b} w powyższym równaniu odpowiedzialne są za kształt spirali: zmiana a spowoduje obrócenie krzywej, a wartość b wyznacza odległość pomiędzy ramionami.

Prosta |

Prosta radialna, tzn. prosta przechodząca przez biegun, jest zadana przez równanie

φ=φ0,{displaystyle varphi =varphi _{0},}

gdzie φ0{displaystyle varphi _{0}} to nachylenie prostej.

Prosta nieradialna, która jest prostopadła do prostej radialnej

φ=φ0{displaystyle varphi =varphi _{0}}

i przecina ją w punkcie (r0,φ0),{displaystyle (r_{0},varphi _{0}),} zadana jest przez równanie

r=r0sec⁡(φ−φ0).{displaystyle r=r_{0}sec(varphi -varphi _{0}).}

Pole powierzchni ograniczonej wykresem funkcji |

Tak jak w układzie kartezjańskim powierzchnię wykresu funkcji f{displaystyle f} można podzielić na prostokąty o wymiarach f(x)×dx,{displaystyle f(x)times dx,} gdzie f(x){displaystyle f(x)} jest wartością funkcji dla argumentu x,{displaystyle x,} zaś dx{displaystyle dx} jest różniczką tegoż argumentu, można poprzez analogię w układzie współrzędnych biegunowych, podzielić powierzchnię wykresu funkcji r{displaystyle r} na trójkąty równoramienne, których wierzchołki zawarte pomiędzy ich ramionami znajdują się w biegunie, drugie są częścią wykresu, zaś trzecie znajdują się obok drugich i jednocześnie w tej samej odległości od bieguna, co te drugie, przy czym długość obu ramion jest równa r(φ),{displaystyle r(varphi ),} gdzie r(φ){displaystyle r(varphi )} jest wartością funkcji dla argumentu φ,{displaystyle varphi ,} zaś kąt zawarty pomiędzy ramionami wynosi dφ,{displaystyle dvarphi ,} gdzie dφ→0{displaystyle dvarphi to 0} jest różniczką tegoż argumentu. Skorzystamy tutaj z jednego ze wzorów na pole powierzchni trójkąta, które jest równe połowie iloczynu długości jego ramion i sinusa kąta zawartego między nimi. W naszym przypadku różniczka powierzchni dS{displaystyle dS} będzie równa:

dS(φ)=12r(φ)r(φ)sin(dφ)=12r2(φ)⋅sin(dφ)dφ⋅dφ{displaystyle dS(varphi )={frac {1}{2}}r(varphi )r(varphi )sin(dvarphi )={frac {1}{2}}r^{2}(varphi )cdot {frac {sin(dvarphi )}{dvarphi }}cdot dvarphi }

Ponieważ limdφ→0sin(dφ)dφ=1,{displaystyle lim _{dvarphi to 0}{frac {sin(dvarphi )}{dvarphi }}=1,} otrzymujemy:

dS(φ)=12r2(φ)dφ{displaystyle dS(varphi )={frac {1}{2}}r^{2}(varphi )dvarphi }

Tak więc pole powierzchni S{displaystyle S} ograniczonej wykresem funkcji r{displaystyle r} wyraża się wzorem:

S=∫αβdS(φ)=∫αβ12r2(φ)dφ=12∫αβr2(φ)dφ{displaystyle S=int _{alpha }^{beta }dS(varphi )=int _{alpha }^{beta }{frac {1}{2}}r^{2}(varphi )dvarphi ={frac {1}{2}}int _{alpha }^{beta }r^{2}(varphi )dvarphi }

Długość łuku wykresu funkcji |

W układzie współrzędnych biegunowych, powierzchnię wykresu funkcji r{displaystyle r} można podzielić na trójkąty, których wierzchołki zawarte pomiędzy ich ramionami O{displaystyle O} znajdują się w biegunie, zaś 2 pozostałe: P{displaystyle P} i Q,{displaystyle Q,} są częścią wykresu i znajdują się obok siebie, przy czym długość pierwszego ramienia |OP|{displaystyle |OP|} wynosi r(φ),{displaystyle r(varphi ),} drugiego |OQ|:{displaystyle |OQ|{:}} r(φ+dφ)=r(φ)+dr(φ){displaystyle r(varphi +dvarphi )=r(varphi )+dr(varphi )} dla argumentu φ,{displaystyle varphi ,} długość podstawy |PQ|{displaystyle |PQ|} jest różniczką naszego łuku, a więc oznaczona jako dL,{displaystyle dL,} zaś kąt zawarty pomiędzy ramionami (POQ){displaystyle (POQ)} wynosi dφ,{displaystyle dvarphi ,} gdzie dφ→0{displaystyle dvarphi to 0} jest różniczką tegoż argumentu. Na ramieniu OQ{displaystyle OQ} umieszczamy punkt R,{displaystyle R,} który dzieli to ramię w ten sposób, że |OR|=|OP|=r(φ),{displaystyle |OR|=|OP|=r(varphi ),} zaś |RQ|=dr(φ).{displaystyle |RQ|=dr(varphi ).} W ten sposób podzieliliśmy trójkąt OPQ{displaystyle OPQ} na 2 mniejsze: równoramienny OPR{displaystyle OPR} (o podstawie PR{displaystyle PR}) i PQR.{displaystyle PQR.} Kąt ORP{displaystyle ORP} oznaczmy jako γ,{displaystyle gamma ,} zaś kąt PRQ{displaystyle PRQ} – jako δ.{displaystyle delta .} Kąty dφ{displaystyle dvarphi } i γ{displaystyle gamma } znajdują się w trójkącie równoramiennym, tak więc suma ich wszystkich jest równa π:{displaystyle pi {:}}

2γ+dφ=π{displaystyle 2gamma +dvarphi =pi }

2γ=π−dφ{displaystyle 2gamma =pi -dvarphi }

γ=π−dφ2{displaystyle gamma ={frac {pi -dvarphi }{2}}}

Ponieważ dφ→0,{displaystyle dvarphi to 0,} więc:

γ→π2{displaystyle gamma to {frac {pi }{2}}}

Kąty γ{displaystyle gamma } i δ{displaystyle delta } są względem siebie przyległe, tak więc ich suma jest równa π:{displaystyle pi {:}}

γ+δ=π{displaystyle gamma +delta =pi }

δ=π−γ=π−π−dφ2=π+dφ2{displaystyle delta =pi -gamma =pi -{frac {pi -dvarphi }{2}}={frac {pi +dvarphi }{2}}}

Ponieważ dφ→0,{displaystyle dvarphi to 0,} więc:

δ→π2{displaystyle delta to {frac {pi }{2}}}

Skoro więc kąt δ{displaystyle delta } znajduje się w trójkącie PQR,{displaystyle PQR,} to trójkąt ten można uznać za prostokątny, a skoro tworzą go boki PQ,{displaystyle PQ,} PR{displaystyle PR} i QR,{displaystyle QR,} to muszą one spełniać twierdzenie Pitagorasa:

|PQ|2=|PR|2+|QR|2{displaystyle |PQ|^{2}=|PR|^{2}+|QR|^{2}}

dL2=|PR|2+dr2(φ){displaystyle dL^{2}=|PR|^{2}+dr^{2}(varphi )}

Długość podstawy |PR|{displaystyle |PR|} można policzyć w oparciu o twierdzenie cosinusów:

|PR|2=r2(φ)+r2(φ)−2r(φ)r(φ)cos(dφ)=2r2(φ)−2r2(φ)cos(dφ)=2r2(φ)(1−cos(dφ)){displaystyle |PR|^{2}=r^{2}(varphi )+r^{2}(varphi )-2r(varphi )r(varphi )cos(dvarphi )=2r^{2}(varphi )-2r^{2}(varphi )cos(dvarphi )=2r^{2}(varphi )(1-cos(dvarphi ))}

Powyższe otrzymane wyrażenie podstawiamy do wcześniejszej zależności wynikającej z twierdzenia Pitagorasa:

dL2=2r2(φ)(1−cos(dφ))+dr2(φ)=(2r2(φ)⋅1−cos(dφ)dφ2+(dr(φ)dφ)2)dφ2=(2r(φ)2⋅1−cos(dφ)dφ2+r′(φ)2)dφ2{displaystyle dL^{2}=2r^{2}(varphi )(1-cos(dvarphi ))+dr^{2}(varphi )=left(2r^{2}(varphi )cdot {frac {1-cos(dvarphi )}{dvarphi ^{2}}}+left({frac {dr(varphi )}{dvarphi }}right)^{2}right)dvarphi ^{2}=left(2r(varphi )^{2}cdot {frac {1-cos(dvarphi )}{dvarphi ^{2}}}+r'(varphi )^{2}right)dvarphi ^{2}}

Ponieważ limdφ→01−cos(dφ)dφ2=12,{displaystyle lim _{dvarphi to 0}{frac {1-cos(dvarphi )}{dvarphi ^{2}}}={frac {1}{2}},} otrzymujemy:

dL2=((⧸2r(φ)2⋅1⧸2+r′(φ)2)dφ2=(r(φ)2+r′(φ)2)dφ2{displaystyle dL^{2}=left((not 2r(varphi )^{2}cdot {frac {1}{not 2}}+r'(varphi )^{2}right)dvarphi ^{2}=(r(varphi )^{2}+r'(varphi )^{2})dvarphi ^{2}}

Tak więc różniczka łuku dL{displaystyle dL} wykresu funkcji r{displaystyle r} w układzie współrzędnych biegunowych wyraża się wzorem:

dL(φ)=r(φ)2+r′(φ)2dφ{displaystyle dL(varphi )={sqrt {r(varphi )^{2}+r'(varphi )^{2}}}dvarphi }

Długość łuku L{displaystyle L} wykresu funkcji r{displaystyle r} wyraża się wzorem:

L=∫αβdL(φ)=∫αβr(φ)2+r′(φ)2dφ{displaystyle L=int _{alpha }^{beta }dL(varphi )=int _{alpha }^{beta }{sqrt {r(varphi )^{2}+r'(varphi )^{2}}}dvarphi }

Liczby zespolone |

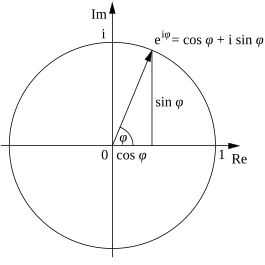
Postaci trygonometryczna i wykładnicza liczb zespolonych

Liczby zespolone mogą być przedstawiane jako punkty na płaszczyźnie zespolonej. Wówczas możemy je opisywać albo używając układu kartezjańskiego:

z=x+iy{displaystyle z=x+iy}

albo podając je w układzie biegunowym, otrzymując tzw. postać trygonometryczną liczby zespolonej z:{displaystyle z{:}}

z=r⋅(cos⁡(φ)+isin⁡(φ)).{displaystyle z=rcdot (cos(varphi )+isin(varphi )).}

(Powyżej, r{displaystyle r} to moduł liczby z,{displaystyle z,} a φ{displaystyle varphi } to jej argument).

Postać trygonometryczna liczby zespolonej jest przekształcana do postaci wykładniczej

z=reiφ,{displaystyle z=re^{ivarphi },}

gdzie e to liczba Eulera.

Użyteczność postaci trygonometrycznej i wykładniczej liczb zespolonych wynika m.in. z faktu, że mnożenie, dzielenie i potęgowanie liczb w tych postaciach jest szczególnie proste:

• r0eiθ0⋅r1eiθ1=r0r1ei(θ0+θ1),{displaystyle r_{0}e^{itheta _{0}}cdot r_{1}e^{itheta _{1}}=r_{0}r_{1}e^{i(theta _{0}+theta _{1})},}


• r0eiθ0r1eiθ1=r0r1ei(θ0−θ1),{displaystyle {frac {r_{0}e^{itheta _{0}}}{r_{1}e^{itheta _{1}}}}={frac {r_{0}}{r_{1}}}e^{i(theta _{0}-theta _{1})},}


• (reiθ)n=rneinθ.{displaystyle (re^{itheta })^{n}=r^{n}e^{intheta }.}

Zobacz też |

• układ współrzędnych astronomicznych


• układ współrzędnych sferycznych


• współrzędne geograficzne

Przypisy |